Difference between revisions of "2016 IMO Problems/Problem 1"
(→Problem) |
(→Solution) |
||
| Line 8: | Line 8: | ||
[[File:2016IMOQ1Solution.jpg|600px]] | [[File:2016IMOQ1Solution.jpg|600px]] | ||
| + | |||
| + | Given \(\angle DAC = \angle DCA = \angle CAD\), it follows that \(AB \parallel CD\). Extend \(DC\) to intersect \(AB\) at \(G\), making \(\angle GFA = \angle GFB = \angle CFD\). Triangles \(\triangle CDF\) and \(\triangle AGF\) are similar. Also, \(\angle FDC = \angle FGA = 90^\circ\) and \(\angle FBC = 90^\circ\), which implies points \(D\), \(C\), \(B\), and \(F\) are concyclic. | ||
| + | |||
| + | Furthermore, \(\angle BFC = \angle FBA + \angle FAB = \angle FAE = \angle AFE\). Triangle \(\triangle AFE\) is congruent to \(\triangle FBM\), and \(AE = EF = FM = MB\). Let \(MX = EA = MF\), then points \(B\), \(C\), \(D\), \(F\), and \(X\) are concyclic. | ||
| + | |||
| + | It is also given that \(AD = DB\) and \(\angle DAF = \angle DBF = \angle FXD\). Additionally, \(\angle MFX = \angle FXD = \angle FXM\) and \(FE \parallel MD\) with \(EF = FM = MD = DE\), making \(EFMD\) a rhombus. Consequently, \(\angle FBD = \angle MBD = \angle MXF = \angle DXF\) and triangle \(\triangle BEM\) is congruent to \(\triangle XEM\), while \(\triangle MFX\) is congruent to \(\triangle MBD\) which is congruent to \(\triangle FEM\), and \(EM = FX = BD\). | ||
| + | |||
| + | ~Athmyx | ||
==See Also== | ==See Also== | ||
{{IMO box|year=2016|before=First Problem|num-a=2}} | {{IMO box|year=2016|before=First Problem|num-a=2}} | ||
Revision as of 11:29, 20 April 2024
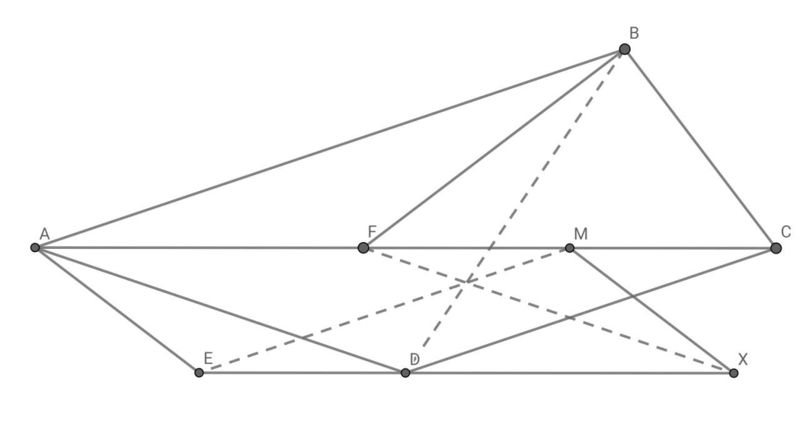
Problem
Triangle 
has a right angle at 
. Let 
be the point on line 
such that 
and 
lies between and 
. Point 
is chosen so that 
and 
is the bisector of 
. Point 
is chosen so that 
and 
is the bisector of 
. Let 
be the midpoint of . Let 
be the point such that 
is a parallelogram. Prove that 
and 
are concurrent.
Solution
Given \(\angle DAC = \angle DCA = \angle CAD\), it follows that \(AB \parallel CD\). Extend \(DC\) to intersect \(AB\) at \(G\), making \(\angle GFA = \angle GFB = \angle CFD\). Triangles \(\triangle CDF\) and \(\triangle AGF\) are similar. Also, \(\angle FDC = \angle FGA = 90^\circ\) and \(\angle FBC = 90^\circ\), which implies points \(D\), \(C\), \(B\), and \(F\) are concyclic.
Furthermore, \(\angle BFC = \angle FBA + \angle FAB = \angle FAE = \angle AFE\). Triangle \(\triangle AFE\) is congruent to \(\triangle FBM\), and \(AE = EF = FM = MB\). Let \(MX = EA = MF\), then points \(B\), \(C\), \(D\), \(F\), and \(X\) are concyclic.
It is also given that \(AD = DB\) and \(\angle DAF = \angle DBF = \angle FXD\). Additionally, \(\angle MFX = \angle FXD = \angle FXM\) and \(FE \parallel MD\) with \(EF = FM = MD = DE\), making \(EFMD\) a rhombus. Consequently, \(\angle FBD = \angle MBD = \angle MXF = \angle DXF\) and triangle \(\triangle BEM\) is congruent to \(\triangle XEM\), while \(\triangle MFX\) is congruent to \(\triangle MBD\) which is congruent to \(\triangle FEM\), and \(EM = FX = BD\).
~Athmyx
See Also
| 2016 IMO (Problems) • Resources | ||
| Preceded by First Problem |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 2 |
| All IMO Problems and Solutions | ||
