Difference between revisions of "2024 AMC 12B Problems/Problem 12"

Latest revision as of 22:02, 25 December 2024

Problem

Suppose $z$ is a complex number with positive imaginary part, with real part greater than $1$ , and with $|z| = 2$ . In the complex plane, the four points $0$ , $z$ , $z^{2}$ , and $z^{3}$ are the vertices of a quadrilateral with area $15$ . What is the imaginary part of $z$ ?

$\textbf{(A) }\frac{3}{4}\qquad\textbf{(B) }1\qquad\textbf{(C) }\frac{4}{3}\qquad\textbf{(D) }\frac{3}{2}\qquad\textbf{(E) }\frac{5}{3}$

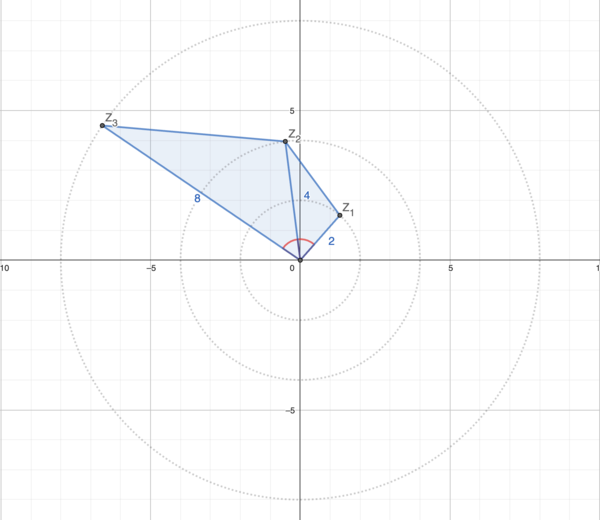
Diagram

Solution 1

By making a rough estimate of where $z$ , $z^2$ , and $z^3$ are on the complex plane, we can draw a pretty accurate diagram (like above.)

Here, points $Z_1$ , $Z_2$ , and $Z_3$ lie at the coordinates of $z$ , $z^2$ , and $z^3$ respectively, and $O$ is the origin.

We're given $|z|=2$ , so $|z^2|=|z|^2=4$ and $|z^3|=|z|^3 = 8$ . This gives us $OZ_1=2$ , $OZ_2=4$ , and $OZ_3=8$ .

Additionally, we know that $\angle{Z_1OZ_2}\cong\angle{Z_2OZ_3}$ (since every power of $z$ rotates around the origin by the same angle.) We set these angles equal to $\theta$ .

We have that \begin{align*} [OZ_1Z_2Z_3]&=[OZ_1Z_2]+[OZ_2Z_3] \\ &=\frac{1}{2}\cdot2\cdot4 \sin\theta+\frac{1}{2}\cdot4\cdot8 \sin\theta \\ &=4\sin\theta+16\sin\theta \\ &=20 \sin\theta \end{align*}

Since this is equal to $15$ , we have $20\sin\theta=15$ , so $\sin\theta=\frac{3}{4}$ .

Thus, $\text{Im}(z)=|z|\sin(\theta)=2(\frac{3}{4})=\boxed{\textbf{(D) }\frac{3}{2}}$ .

~nm1728, ShortPeopleFartalot

Solution 2 (Shoelace Theorem)

We have the vertices:

$0$ at $(0, 0)$ , $z$ at $(2\cos \theta, 2\sin \theta)$ , $z^2$ at $(4\cos 2\theta, 4\sin 2\theta)$ , $z^3$ at $(8\cos 3\theta, 8\sin 3\theta)$

The Shoelace formula for the area is: $= \frac{1}{2} \left| x_1 y_2 + x_2 y_3 + x_3 y_4 + x_4 y_1 - (y_1 x_2 + y_2 x_3 + y_3 x_4 + y_4 x_1) \right|.$ $= \frac{1}{2} \left| 0 + 2\cos \theta \cdot 4\sin 2\theta + 4\cos 2\theta \cdot 8\sin 3\theta - (2\sin \theta \cdot 4\cos 2\theta + 4\sin 2\theta \cdot 8\cos 3\theta) \right|.$ $= \frac{1}{2} \left| 8\cos \theta \sin 2\theta + 32\cos 2\theta \sin 3\theta - 8\sin \theta \cos 2\theta - 32\sin 2\theta \cos 3\theta \right|$ $= \frac{1}{2} \left|(8\cos \theta \sin 2\theta - 8\sin \theta \cos 2\theta) + (32\cos 2\theta \sin 3\theta - 32\sin 2\theta \cos 3\theta) \right|$ $= \frac{1}{2} \left|8\sin(2\theta - \theta) + 32\sin(2\theta - \theta) \right|$ $= \frac{1}{2} \left| 8\sin \theta + 32\sin \theta \right|$ $= \frac{1}{2} \left| 40\sin \theta \right|$ Given that the area is 15: $\frac{1}{2} \left| 40\sin \theta \right| = 15.$ $20|\sin \theta| = 15 \implies |\sin \theta| = \frac{3}{4}.$ Since $\theta$ corresponds to a complex number $z$ with a positive imaginary part, we have:

$\sin \theta = \frac{3}{4}.$ $\text{Imaginary part} = 2\sin \theta = 2 \times \frac{3}{4} = \boxed{\textbf{(D) }\frac{3}{2}}.$

~luckuso

Solution 3 (No Trig)

Let $z = a + bi$ , so $z^2 = a^2 + 2abi - b^2$ and $z^3 = a^3 + 3a^2 bi - 3ab^2 - b^3 i$ . Therefore, converting $0, z, z^2, z^3$ from complex coordinates to Cartesian coordinates gives us the following.

$(0, 0)$

$(a, b)$

$(a^2 - b^2, 2ab)$

$(a^3 - 3ab^2, 3a^2 b - b^3)$

The Shoelace Theorem tells us that the area is

$\frac{1}{2} \Bigg| \Big[ (0)(b) + (a)(2ab) + (a^2 - b^2)(3a^2 b - b^3) + (a^3 - 3ab^2)(0) \Big] - \Big[ (0)(a) + (b)(a^2 - b^2) + (2ab)(a^3 - 3ab^2) + (3a^2 b - b^3)(0) \Big] \Bigg|$

$= \frac{1}{2} \Bigg| \Big[ (0) + (2a^2 b) + (3a^4 b - a^2 b^3 - 3a^2 b^3 + b^5) + (0) \Big] - \Big[ (0) + (a^2 b - b^3) + (2a^4 b - 6a^2 b^3) + (0) \Big] \Bigg|$

$= \frac{1}{2} \Big| [3a^4 b - 4a^2 b^3 + b^5 + 2a^2 b] - [2a^4 b - 6a^2 b^3 + a^2 b - b^3] \Big|$

$= \frac{1}{2} | a^4 b + 2a^2 b^3 + b^5 + a^2 b + b^3 |.$

We know that $|z| = |a + bi| = \sqrt{a^2 + b^2} = 2$ , so $a^2 = 4 - b^2$ . Substituting this gives us this:

$\frac{1}{2} \Big| (4 - b^2)^2 b + 2(4 - b^2)b^3 + b^5 + (4 - b^2)b + b^3 \Big|$

$= \frac{1}{2} \Big| (16b - 8b^3 + b^5) + (8b^3 - 2b^5) + b^5 + (4b - b^3) + b^3 \Big|$

$= \frac{1}{2} | 0b^5 + 0b^3 + 20b|$

$= 15.$

In other words,

$|10b| = 15$

$b = \textbf{(D) } \frac{3}{2}.$

Solution 4

Video Solution 1 by SpreadTheMathLove

https://www.youtube.com/watch?v=OMR5MYtu11s&t=0s

@@ Line 30: / Line 30: @@
 Thus, <math>\text{Im}(z)=|z|\sin(\theta)=2(\frac{3}{4})=\boxed{\textbf{(D) }\frac{3}{2}}</math>.
-~nm1728
+~nm1728, ShortPeopleFartalot
 ==Solution 2 (Shoelace Theorem)==

2024 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 11	Followed by Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search