Difference between revisions of "Trigonometric identities"
(→Double Angle Identities) |
m (→Further Conclusions) |
||
| Line 31: | Line 31: | ||
Based on the above identities, we can also claim that | Based on the above identities, we can also claim that | ||
| − | *<math>sin(cos(-\theta)) = sin(cos(\theta))</math> | + | *<math>\sin(\cos(-\theta)) = \sin(\cos(\theta))</math> |
| − | *<math>cos(sin(-\theta)) = cos(-sin(\theta)) = cos(sin(\theta))</math> | + | *<math>\cos(\sin(-\theta)) = \cos(-\sin(\theta)) = \cos(\sin(\theta))</math> |
| − | This is only true when <math>sin(\theta)</math> is in the domain of <math>cos(\theta)</math>. | + | This is only true when <math>\sin(\theta)</math> is in the domain of <math>\cos(\theta)</math>. |
== Reciprocal Relations == | == Reciprocal Relations == | ||
Revision as of 23:10, 14 August 2011
Trigonometric identities are used to manipulate trigonometry equations in certain ways. Here is a list of them:
Contents
[hide]Basic Definitions
The six basic trigonometric functions can be defined using a right triangle:
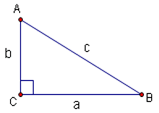
The six trig functions are sine, cosine, tangent, cosecant, secant, and cotangent. They are abbreviated by using the first three letters of their name (except for cosecant which uses ![]() ). They are defined as follows:
). They are defined as follows:
Even-Odd Identities
Further Conclusions
Based on the above identities, we can also claim that
This is only true when ![]() is in the domain of
is in the domain of ![]() .
.
Reciprocal Relations
From the last section, it is easy to see that the following hold:
Another useful identity that isn't a reciprocal relation is that ![]() .
.
Note that ![]() ; the former refers to the inverse trigonometric functions.
; the former refers to the inverse trigonometric functions.
Pythagorean Identities
Using the Pythagorean Theorem on our triangle above, we know that ![]() . If we divide by
. If we divide by ![]() we get
we get ![]() , which is just
, which is just ![]() . Dividing by
. Dividing by ![]() or
or ![]() instead produces two other similar identities. The Pythagorean Identities are listed below:
instead produces two other similar identities. The Pythagorean Identities are listed below:
(Note that the second two are easily derived by dividing the first by ![]() and
and ![]() )
)
Angle Addition/Subtraction Identities
Once we have formulas for angle addition, angle subtraction is rather easy to derive. For example, we just look at ![]() and we can derive the sine angle subtraction formula using the sine angle addition formula.
and we can derive the sine angle subtraction formula using the sine angle addition formula.
We can prove ![]() easily by using
easily by using ![]() and
and ![]() .
.
![]()
![]()
![]()
![]()
Double Angle Identities
Double angle identities are easily derived from the angle addition formulas by just letting ![]() . Doing so yields:
. Doing so yields:
$\begin{eqnarray*} \sin 2\alpha &=& 2\sin \alpha \cos \alpha\ \cos 2\alpha &=& \cos^2 \alpha - \sin^2 \alpha\ &=& 2\cos^2 \alpha - 1\ &=& 1-2\sin^2 \alpha\ \tan 2\alpha &=& \frac{2\tan \alpha}{1-\tan^2\alpha}$ (Error compiling LaTeX. Unknown error_msg)
Further Conclusions
We can see from the above that
Half Angle Identities
Using the double angle identities, we can now derive half angle identities. The double angle formula for cosine tells us ![]() . Solving for
. Solving for ![]() we get
we get ![]() where we look at the quadrant of
where we look at the quadrant of ![]() to decide if it's positive or negative. Likewise, we can use the fact that
to decide if it's positive or negative. Likewise, we can use the fact that ![]() to find a half angle identity for sine. Then, to find a half angle identity for tangent, we just use the fact that
to find a half angle identity for sine. Then, to find a half angle identity for tangent, we just use the fact that ![]() and plug in the half angle identities for sine and cosine.
and plug in the half angle identities for sine and cosine.
To summarize:
Prosthaphaeresis Identities
(Otherwise known as sum-to-product identities)
Law of Sines
- Main article: Law of Sines
The extended Law of Sines states
Law of Cosines
- Main article: Law of Cosines
The Law of Cosines states
Law of Tangents
- Main article: Law of Tangents
The Law of Tangents states that if ![]() and
and ![]() are angles in a triangle opposite sides
are angles in a triangle opposite sides ![]() and
and ![]() respectively, then
respectively, then
![]()
Other Identities
 (This is also written as
(This is also written as  )
)
- $\Left(\tan\theta + \sec\theta\Right)^2 = \frac{1 + \sin\theta}{1 - \sin\theta}$ (Error compiling LaTeX. Unknown error_msg)





The two identities right above here were based on identites others posted on this site with a substitution.









