Difference between revisions of "Angle Bisector Theorem"

Revision as of 16:22, 24 June 2006

Introduction

The Angle Bisector Theorem states that given triangle $\triangle ABC$ and angle bisector AD, where D is on side BC, then $\frac cm = \frac bn$ .

Proof

Method 1

Because of the ratios and equal angles in the theorem, we think of similar triangles. There are not any similar triangles in the figure as it now stands, however. So we think to draw in a carefully chosen line or two. Extending AD until it hits the line through C parallel to AB does just the trick as we shall see!

Since AB and CE are parallel, we know that $\angle BAE \cong \angle CEA$ and $\angle BCE \cong \angle ABC$ . Triangle ACE is isosceles meaning that AC = CE.

By AA, $\triangle DAB \cong \triangle DEC$ . By the properties of similar triangles, we arrive at our desired result:

$\frac cm = \frac bn.$

Method 2

Let $AD = d$ . Now, we can express the area of triangle ABD in two ways:

$[ABD] = \frac 12 cd\sin \angle BAD = \frac 12 md \sin \angle ADB.$

Thus $\frac{\sin \angle ADB}{\sin \angle BAD} = \frac cm$ .

Likewise, triangle ACD can be expressed in two different ways:

$[ACD] = \frac 12 bd \sin \angle CAD = \frac 12 dn \sin \angle ADC.$

Thus $\frac{\sin \angle ADC}{\sin \angle CAD} = \frac bn$ .

But $\angle CAD \cong \angle BAD$ and $\sin \angle ADC = \sin \angle ADB$ since $\angle ADC = \pi - \angle ADB$ . Therefore, we can substitute back into our previous equation to get $\frac{\sin \angle ADB}{\sin \angle BAD} = \frac bn$ .

We conclude that $\frac{\sin \angle ADB}{\sin \angle BAD} = \frac cm = \frac bn$ , which was what we wanted.

@@ Line 1: / Line 1: @@
-The '''Angle Bisector Theorem''' states that given [[triangle]] <math>\triangle ABC</math> and [[angle bisector]] AX, where X is on side BC,  then <math>AC/CX = AB/BX</math>.
+== Introduction ==
+The '''Angle Bisector Theorem''' states that given [[triangle]] <math>\triangle ABC</math> and [[angle bisector]] AD, where D is on side BC,  then <math> \frac cm = \frac bn </math>.
 <center>[[Image:Anglebisector.png]]</center>
-{{stub}}
+== Proof ==
+===Method 1 ===
+Because of the ratios and equal angles in the theorem, we think of similar triangles.  There are not any similar triangles in the figure as it now stands, however.  So we think to draw in a carefully chosen line or two.  Extending AD until it hits the line through C parallel to AB does just the trick as we shall see!
+<center>[[image:Anglebisectortheorem.PNG]]</center>
+Since AB and CE are parallel, we know that <math> \angle BAE \cong \angle CEA </math> and <math> \angle BCE \cong \angle ABC </math>.  Triangle ACE is isosceles meaning that AC = CE.
+By AA, <math> \triangle DAB \cong \triangle DEC </math>.  By the properties of similar triangles, we arrive at our desired result:
+<center><math> \frac cm = \frac bn.</math> </center>
+=== Method 2 ===
+Let <math> AD = d </math>.  Now, we can express the area of triangle ABD in two ways:
+<center><math> [ABD] = \frac 12 cd\sin \angle BAD = \frac 12  md \sin \angle ADB. </math></center>
+Thus <math> \frac{\sin \angle ADB}{\sin \angle BAD} = \frac cm </math>.
+Likewise, triangle ACD can be expressed in two different ways:
+<center><math> [ACD] = \frac 12 bd \sin \angle CAD = \frac 12 dn \sin \angle ADC. </math></center>
+Thus <math> \frac{\sin \angle ADC}{\sin \angle CAD} = \frac bn</math>.
+But <math> \angle CAD \cong \angle BAD </math> and <math> \sin \angle ADC = \sin \angle ADB </math> since <math> \angle ADC = \pi - \angle ADB </math>.  Therefore, we can substitute back into our previous equation to get <math> \frac{\sin \angle ADB}{\sin \angle BAD} = \frac bn </math>.
+We conclude that <math> \frac{\sin \angle ADB}{\sin \angle BAD} = \frac cm = \frac bn </math>, which was what we wanted.
+== Examples ==
+== See also ==
+* [[Angle bisector]]
+* [[Geometry]]
+* [[Stewart's Theorem]]

Page

Toolbox

Search

Difference between revisions of "Angle Bisector Theorem"

Revision as of 16:22, 24 June 2006

Contents

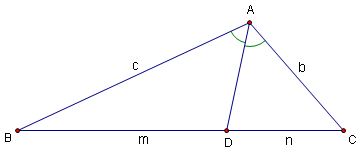
Introduction

Proof

Method 1

Method 2

Examples

See also