Difference between revisions of "1992 AIME Problems/Problem 10"
(Undo revision 71029 by Starwars123 (talk)) |
(Undo revision 71028 by Starwars123 (talk)) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| + | Consider the region <math>A</math> in the complex plane that consists of all points <math>z</math> such that both <math>\frac{z}{40}</math> and <math>\frac{40}{\overline{z}}</math> have real and imaginary parts between <math>0</math> and <math>1</math>, inclusive. What is the integer that is nearest the area of <math>A</math>? | ||
| + | (If <math>z=a+bi</math> with <math>a</math> and <math>b</math> real, then <math>z=a-bi</math> is the conjugate of <math>z</math>) | ||
== Solution == | == Solution == | ||
Revision as of 12:37, 8 July 2015
Problem
Consider the region ![]() in the complex plane that consists of all points
in the complex plane that consists of all points ![]() such that both
such that both ![]() and
and ![]() have real and imaginary parts between
have real and imaginary parts between ![]() and
and ![]() , inclusive. What is the integer that is nearest the area of
, inclusive. What is the integer that is nearest the area of ![]() ?
(If
?
(If ![]() with
with ![]() and
and ![]() real, then
real, then ![]() is the conjugate of
is the conjugate of ![]() )
)
Solution
Let ![]() . Since
. Since ![]() we have the inequality
we have the inequality ![]() which is a square of side length
which is a square of side length ![]() .
.
Also, ![]() so we have
so we have ![]() , which leads to:
, which leads to:![]()
![]()
We graph them:
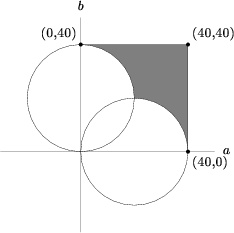
We want the area outside the two circles but inside the square. Doing a little geometry, the area of the intersection of those three graphs is ![]()
![]()









