1992 AIME Problems/Problem 10
Problem
Consider the region ![]() in the complex plane that consists of all points
in the complex plane that consists of all points ![]() such that both
such that both ![]() and
and ![]() have real and imaginary parts between
have real and imaginary parts between ![]() and
and ![]() , inclusive. What is the integer that is nearest the area of
, inclusive. What is the integer that is nearest the area of ![]() ?
?
Solution
Let ![]() . Since
. Since ![]() we have the inequality
we have the inequality ![]() which is a square of side length
which is a square of side length ![]() .
.
Also, ![]() so we have
so we have ![]() , which leads to:
, which leads to:![]()
![]()
We graph them:
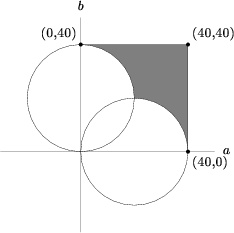
To find the area outside the two circles but inside the square, we want to find the unique area of the two circles. We can do this by adding the area of the two circles and then subtracting out their overlap. There are two methods of finding the area of overlap:
1. Consider that the area is just the quarter-circle with radius ![]() minus an isosceles right triangle with base length
minus an isosceles right triangle with base length ![]() , and then doubled (to consider the entire overlapped area)
, and then doubled (to consider the entire overlapped area)
2. Consider that the circles can be converted into polar coordinates, and their equations are ![]() and
and ![]() . Using calculus with the appropriate bounds, we can compute the overlapped area.
. Using calculus with the appropriate bounds, we can compute the overlapped area.
Using either method, we compute the overlapped area to be ![]() , and so the area of the intersection of those three graphs is
, and so the area of the intersection of those three graphs is ![]()
![]()
See also
| 1992 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()









