Difference between revisions of "Stewart's Theorem"
m (proofreading) |
|||
| Line 8: | Line 8: | ||
== Proof == | == Proof == | ||
| − | For this proof we will use the law of cosines and the identity <math>\cos{\theta} = -\cos{(180 - \theta)}</math>. | + | For this proof, we will use the law of cosines and the identity <math>\cos{\theta} = -\cos{(180 - \theta)}</math>. |
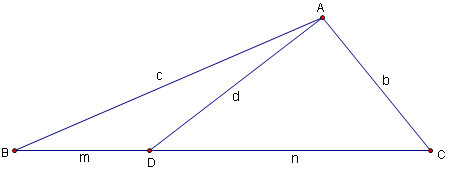
| − | Label the triangle <math>ABC</math> with a cevian extending from <math>A</math> onto <math>BC</math>, label that point <math>D</math>. Let CA = n Let DB = m. Let AD = d. We can write two equations: | + | Label the triangle <math>ABC</math> with a cevian extending from <math>A</math> onto <math>BC</math>, label that point <math>D</math>. Let CA = n. Let DB = m. Let AD = d. We can write two equations: |
*<math> n^{2} + d^{2} - nd\cos{\angle CDA} = b^{2} </math> | *<math> n^{2} + d^{2} - nd\cos{\angle CDA} = b^{2} </math> | ||
*<math> m^{2} + d^{2} + md\cos{\angle CDA} = c^{2} </math> | *<math> m^{2} + d^{2} + md\cos{\angle CDA} = c^{2} </math> | ||
| Line 17: | Line 17: | ||
*<math> \frac{c^2 - m^2 -d^2}{md} = \cos{\angle CDA}</math> | *<math> \frac{c^2 - m^2 -d^2}{md} = \cos{\angle CDA}</math> | ||
| − | Now we set the two equal and arrive at Stewart's theorem: <math> c^{2}n + b^{2}m=m^{2}n +n^{2}m + d^{2}m + d^{2}n </math> | + | Now we set the two equal and arrive at Stewart's theorem: <math> c^{2}n + b^{2}m=m^{2}n +n^{2}m + d^{2}m + d^{2}n </math>. |
== See also == | == See also == | ||
Revision as of 13:05, 17 July 2006
Statement
If a cevian of length d is drawn and divides side a into segments m and n, then
Proof
For this proof, we will use the law of cosines and the identity ![]() .
.
Label the triangle ![]() with a cevian extending from
with a cevian extending from ![]() onto
onto ![]() , label that point
, label that point ![]() . Let CA = n. Let DB = m. Let AD = d. We can write two equations:
. Let CA = n. Let DB = m. Let AD = d. We can write two equations:
When we write everything in terms of cos(CDA) we have:
Now we set the two equal and arrive at Stewart's theorem: ![]() .
.









