2020 AIME I Problems/Problem 1

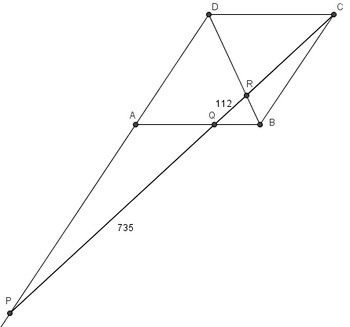
Problem

Let $ABCD$ be a parallelogram. Extend $\overline{DA}$ through $A$ to a point $P,$ and let $\overline{PC}$ meet $\overline{AB}$ at $Q$ and $\overline{DB}$ at $R.$ Given that $PQ = 735$ and $QR = 112,$ find $RC.$

Solution

Solution 1

There are several similar triangles. $\triangle PAQ\sim \triangle PDC$ , so we can write the proportion:

$\frac{AQ}{CD} = \frac{PQ}{PC} = \frac{735}{112 + 735 + RC} = \frac{735}{847 + RC}$

Also, $\triangle BRQ\sim DRC$ , so:

$\frac{QR}{RC} = \frac{QB}{CD} = \frac{112}{RC} = \frac{CD - AQ}{CD} = 1 - \frac{AQ}{CD}$

$\frac{AQ}{CD} = 1 - \frac{112}{RC} = \frac{RC - 112}{RC}$

Substituting,

$\frac{AQ}{CD} = \frac{735}{847 + RC} = \frac{RC - 112}{RC}$

$735RC = (RC + 847)(RC - 112)$
$0 = RC^2 - 112\cdot847$

Thus, $RC = \sqrt{112*847} = 308$ .

Solution 2

We have $\triangle BRQ\sim \triangle DRC$ so $\frac{112}{RC} = \frac{BR}{DR}$ . We also have $\triangle BRC \sim \triangle DRP$ so $\frac{ RC}{847} = \frac {BR}{DR}$ . Equating the two results gives $\frac{13}{RC} = \frac{ RC}{17797}$ and so $RC^2=13*17797$ which solves to $RC=\boxed{481}$

Page

Toolbox

Search

2020 AIME I Problems/Problem 1

Contents

Problem

Solution

Solution 1

Solution 2