1989 AIME Problems/Problem 12
Problem
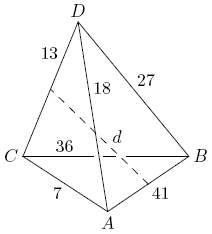
Let ![]() be a tetrahedron with
be a tetrahedron with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , as shown in the figure. Let
, as shown in the figure. Let ![]() be the distance between the midpoints of edges
be the distance between the midpoints of edges ![]() and
and ![]() . Find
. Find ![]() .
.
Solution
Call the midpoint of ![]()
![]() and the midpoint of
and the midpoint of ![]()
![]() .
. ![]() is the median of triangle
is the median of triangle ![]() . The formula for the length of a median is
. The formula for the length of a median is ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are the side lengths of triangle, and
are the side lengths of triangle, and ![]() is the side that is bisected by median
is the side that is bisected by median ![]() . The formula is a direct result of the Law of Cosines applied twice with the angles formed by the median (Stewart's Theorem).
. The formula is a direct result of the Law of Cosines applied twice with the angles formed by the median (Stewart's Theorem).
We first find ![]() , which is the median of
, which is the median of ![]() .
.
![]()
Now we must find ![]() , which is the median of
, which is the median of ![]() .
.
![]()
Now that we know the sides of ![]() , we proceed to find the length of
, we proceed to find the length of ![]() .
.
![]()
See also
| 1989 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||