Stewart's Theorem

Statement

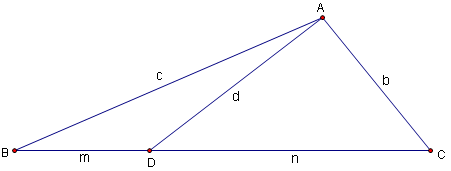
If a cevian of length d is drawn and divides side a into segments m and n, then

$cnc + bmb = man + dad.$

Proof

For this proof, we will use the law of cosines and the identity $\cos{\theta} = -\cos{(180 - \theta)}$ .

Label the triangle $ABC$ with a cevian extending from $A$ onto $BC$ , label that point $D$ . Let CA = n. Let DB = m. Let AD = d. We can write two equations:

$n^{2} + d^{2} - nd\cos{\angle CDA} = b^{2}$
$m^{2} + d^{2} + md\cos{\angle CDA} = c^{2}$

When we write everything in terms of cos(CDA) we have:

$\frac{n^2 + d^2 - b^2}{nd} = \cos{\angle CDA}$
$\frac{c^2 - m^2 -d^2}{md} = \cos{\angle CDA}$

Now we set the two equal and arrive at Stewart's theorem: $c^{2}n + b^{2}m=m^{2}n +n^{2}m + d^{2}m + d^{2}n$ . However, since $m+n$ can be written as a, we get the more common form: $cnc+bmb=man+dad$

Page

Toolbox

Search

Stewart's Theorem

Statement

Proof

See also