Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Polya’s method for extremums

Revision as of 10:55, 22 February 2024 by Vvsss (talk | contribs) (→‎The smallest inscribed equilateral triangle)

The segment of the shortest length

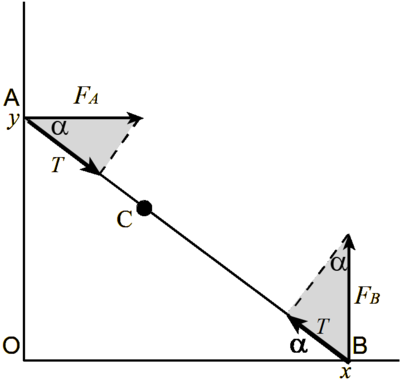
Shortest segment.png

The segment $AB$ has the ends on the sides of a right angle and contains a point $C(x_C, y_C).$ Find the shortest length of such a segment.

Solution

Let's imagine that $AB$ is a spring rod that cannot bend, but tends to shorten its length.

The rod is fixed at point $C$ on a hinge without friction. The hinge allows the rod to rotate and slide.

The ends of the rod can slide without friction along the grooves - the sides of the corner.

Let the rod be balanced, and the force pulling it together is equal to $T.$ The grooves can create a force only along the normal, so they act on the rod with forces \[F_B = \frac {T}{\sin \alpha}, F_A = \frac {T}{\cos \alpha}.\] For the rod to be balanced, it is required that the moments of the forces be equal relative to point $C.$ The moments of forces are: \[F_A \cdot AC \cdot \sin \alpha = F_B \cdot BC \cdot \cos \alpha \implies \frac {BC}{AC} = \tan^2 \alpha,\] \[\frac {y_C}{x_C} = \frac {BC \cdot \sin \alpha}{AC \cdot \cos \alpha} = \tan^3 \alpha \implies\] \[AB = \left ( x_C^ {\frac {2}{3}} + y_C^ {\frac {2}{3}}\right ) ^{\frac {3}{2}}.\] vladimir.shelomovskii@gmail.com, vvsss



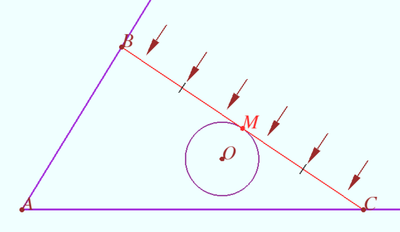
The circle inside a fixed plane angle

Circle and triangle.png

Let the plane angle with vertex $A$ and the circle inside the angle be given. A straight line is drawn through point M of this circle, tangent to the circle and intersecting the sides of the angle at points $B$ and $C.$ Find the condition under which the area of $\triangle ABC$ is the smallest.

Solution

Let us imagine that $AB$ is a rod that cannot bend, and whose ends slide freely along the sides of the angle, and at point $M$ it rests on a convex curve.

Let $\triangle ABC$ be covered with a soap film, which, as usual, tends to reduce its area proportional to the energy. Let ABC be a section of a triangular prism, two faces of which AB and AC are fixed, and the third (BC) is a piston whose width can be changed so that it fits hermetically to the faces AB and AC and can slide along them. The piston rests on a cylinder whose cross-section is a circle with center O.

Air has been removed from the prism. External air presses on the piston and it comes to an equilibrium position. In this case, the energy of the system will be minimal if the volume of the prism becomes minimal. In the equilibrium position, the moments of forces applied to the piston $BC$ on the segments $BM$ and $MC$ are equal. These moments are proportional to the square of the length of the segment, that is, the equilibrium condition is the equality $BM = MC$ or $M$ is the midpoint $BC$ (the center of mass of a homogeneous segment $BC.$)

vladimir.shelomovskii@gmail.com, vvsss

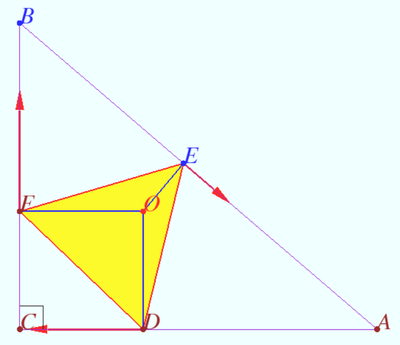
The sphere inside a fixed trihedral angle

There is a sphere inside a fixed trihedral angle with vertex $A.$ A plane is drawn through point $M$ of this sphere, tangent to the sphere and intersecting the edges of the angle at points $B, C,$ and $D.$

Find the condition under which the volume of the pyramid $ABCD$ is the smallest.

Solution

Let us imagine the plane $BCD$ in the form of the piston covering the evacuated volume $ABCD.$ There is no friction of the piston against the walls.

In the equilibrium position, the volume of the evacuated part of the system is minimal. The equilibrium condition is the equality of the moments of pressure forces, which is equivalent to the equality of the moments of gravity for a homogeneous plate $BCD.$ So the point $M$ of the contact with the sphere (or any convex solid) must be at the center of mass of the polygon $BCD.$

vladimir.shelomovskii@gmail.com, vvsss

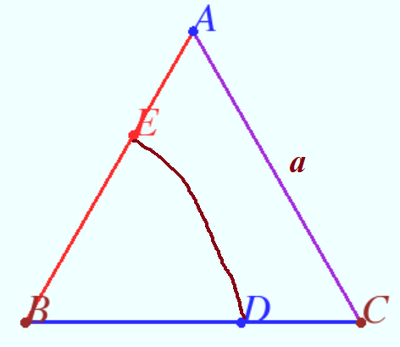
The smallest inscribed equilateral triangle

Rotation triangle.png

A right triangle with sides $a$ and $b$ be given. Find the area of the smallest regular triangle that can be inscribed in it. All vertices of the required triangle must be located on different sides of this triangle.

Solution

Let's imagine the desired triangle as a cross-section of a drill drilling the plane of a given triangle. The axis of rotation does not have to be in the center of the desired triangle.

Let's turn the drill at a small angle clockwise so that the points of the drill touching the sides of this triangle move along the sides.

The required triangle is minimal, which means that all its vertices cannot lie on its sides. One or more will go inside. When turning counterclockwise the situation is similar.

This means that there is an instantaneous axis of rotation of the drill for such turns. Since the required regular triangle is pedal for a point on the instantaneous axis of rotation, this point is the first Apollonius point of given triangle.

Using the properties of this point, we find that the required area is \[\frac {\sqrt{3}}{4} \frac { a^2 b^2}{a^2 + b^2 + \sqrt{3}ab}.\] vladimir.shelomovskii@gmail.com, vvsss

Curve of the smallest length

Shortest line in triangle B.png

Find the length of the curve of the smallest length dividing a given equilateral triangle with side $a$ into two equal parts.

Solution

Note that the shortest (continuous) curve has ends $D$ and $E$ on two sides of the triangle, which we will call blue and red. Let us denote the common vertex of these two sides as $B.$

Let us consider a set of six identical regular triangles in each of which the desired (identical!) curve is drawn.

We place the first of them in an arbitrary way in a certain plane.

We apply the second triangle to the first in the same plane so that the two blue sides and common vertices $B$ of these triangles coincide. In this case, the ends $D$ of the curve on the blue line will coincide, that is, the set of these two curves is also a continuous curve.

We will apply the third triangle to the second so that the red sides, vertices $B$ and points $E$ are coincide. We will similarly apply the fourth, fifth and sixth triangles.

As a result, we obtain a regular hexagon formed by sides opposite to vertex $B,$ inside which a continuous curve limits an area whose area is equal to half the area of the hexagon. It is equal to the area of the three given triangles. It is clear that this is a circle, its area (and radius) are known. The required length of the curve is a sixth of the length of its circumference. \[\pi r^2 = \frac {3 \sqrt {3}}{4} a^2 \implies l = \frac{\pi r}{3} = \frac {a \sqrt{\pi}}{2 \sqrt[4]{3}}\]

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Polya’s_method_for_extremums&oldid=216036"