1988 AIME Problems/Problem 12
Problem
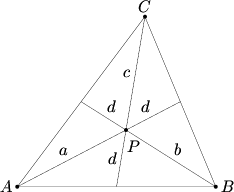
Let ![]() be an interior point of triangle
be an interior point of triangle ![]() and extend lines from the vertices through
and extend lines from the vertices through ![]() to the opposite sides. Let
to the opposite sides. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() denote the lengths of the segments indicated in the figure. Find the product
denote the lengths of the segments indicated in the figure. Find the product ![]() if
if ![]() and
and ![]() .
.
Solution
Call the cevians AD, BE, and CF. Using area ratios (![]() and
and ![]() have the same base), we have:
have the same base), we have:
![]()
Similarily, ![]() and
and ![]() .
.
Then,
![]()
The identity ![]() is a form of Ceva's Theorem.
is a form of Ceva's Theorem.
Plugging in ![]() , we get
, we get
![]()
![]()
![]()
![]()
![]()
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||