2005 AMC 10A Problems/Problem 17
Problem
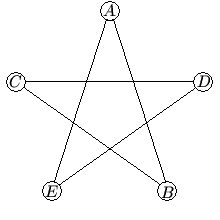
In the five-sided star shown, the letters 
, 
, 
, 
, and 
are replaced by the numbers 
, 
, 
, 
, and 
, although not necessarily in this order. The sums of the numbers at the ends of the line segments 
, 
, 
, 
, and 
form an arithmetic sequence, although not necessarily in this order. What is the middle term of the sequence?
Solution
Since each number is part of 
numbers in the arithmetic sequence, the sum of the arithmetic sequence is 
Since the middle term in an arithmetic sequence is the average of the terms, the middle number is 
