2021 USAJMO Problems/Problem 2
Revision as of 14:00, 15 April 2021 by Leonard my dude (talk | contribs)
Problem
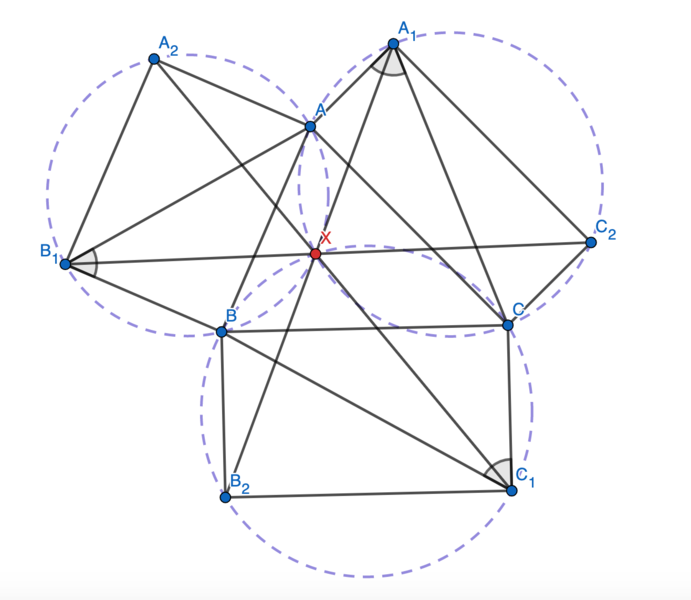
Rectangles ![]()
![]() and
and ![]() are erected outside an acute triangle
are erected outside an acute triangle ![]() Suppose that
Suppose that![]() Prove that lines
Prove that lines ![]()
![]() and
and ![]() are concurrent.
are concurrent.
Solution
We first claim that the three circles ![]()
![]() and
and ![]() are share a common intersection.
are share a common intersection.
Let the second intersection of ![]() and
and ![]() be
be ![]() . Then
. Then
 which implies that
which implies that ![]() is cyclic as desired.
is cyclic as desired.
Now we show that ![]() is the intersection of
is the intersection of ![]()
![]() and
and ![]() Note that
Note that ![]() so
so ![]() are collinear. Similarly,
are collinear. Similarly, ![]() and
and ![]() are collinear, so the three lines concur and we are done.
are collinear, so the three lines concur and we are done.
~Leonard_my_dude