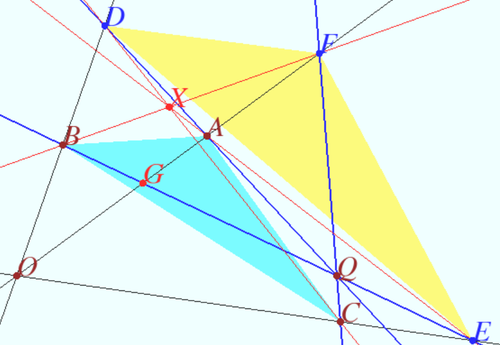
Double perspective triangles
Double perspective triangles
Two triangles in double perspective are in triple perspective
Let 
and 
be in double perspective, which means that triples of lines 
and 
are concurrent. Prove that lines 
and 
are concurrent (the triangles are in triple perspective).
Proof
Denote 
It is known that there is projective transformation that maps any quadrungle into square.
We use this transformation for 
. We use the claim and get the result: lines and are concurrent.
