User talk:Etmetalakret
AoPS Wiki users, ignore this page. I'm using my User Talk to explain proof writing to friends.
Contents
[hide]Proof 1: The Pythagorean Theorem
Prove the Pythagorean Theorem for a right triangle ![]() such that
such that ![]() .
.
Explanation
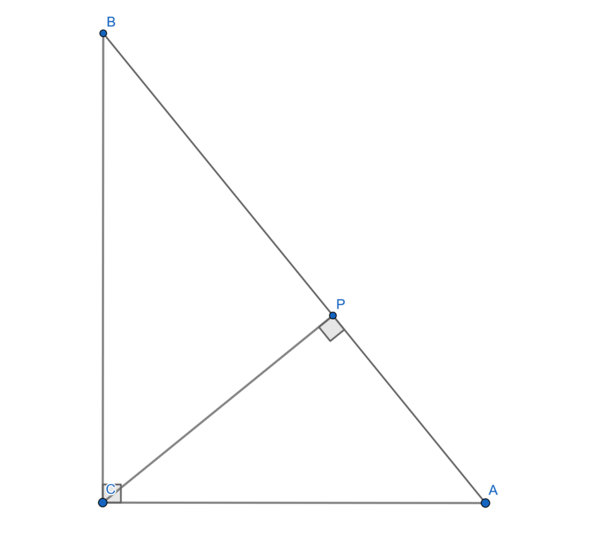
I showed this proof in the study group one time. We let ![]() be an altitude of
be an altitude of ![]() and hunt for triangle similarity. See the following diagram:
and hunt for triangle similarity. See the following diagram:
We let ![]() ,
, ![]() , and
, and ![]() .
.
Examine the triangles ![]() and
and ![]() . They both share
. They both share ![]() and a right angle, so AA Similarity guarantees that
and a right angle, so AA Similarity guarantees that ![]() . Similarly,
. Similarly, ![]() . We thus get the following ratios:
. We thus get the following ratios: ![]() We can solve for
We can solve for ![]() and
and ![]() as follows:
as follows: ![]() But why is this useful? It's because
But why is this useful? It's because ![]() . Using this fact, we have that
. Using this fact, we have that ![]() Multiplying this equation by
Multiplying this equation by ![]() yields the desired
yields the desired ![]() .
.
Bad Proof
Note that ![]() and
and ![]() . We thus have by AA Similarity that
. We thus have by AA Similarity that ![]() . Similarly,
. Similarly, ![]() . Therefore,
. Therefore, ![]() We can solve for
We can solve for ![]() and
and ![]() as follows:
as follows: ![]() Then the following sequence of equations holds:
Then the following sequence of equations holds: ![]() Multiplying this equation by
Multiplying this equation by ![]() yields the desired
yields the desired ![]() .
. ![]()
Why is this proof bad?
- No Diagram: You ALWAYS need a diagram in geometry proofs to help the grader remain oriented in dense notation.
- Terms have not been defined: What are
 ,
,  , and
, and  ? What about
? What about  ? You can still use these these instead of writing out
? You can still use these these instead of writing out  ,
,  ,
,  , and
, and  , but you need to define them.
, but you need to define them. - Not Enough Space: GIVE THESE WALLS OF EQUATIONS THEIR OWN LINES!
- Degrees Not Specified: The proof references
 , not whatever
, not whatever  means.
means.
Good Proof
Let ![]() be the point on
be the point on ![]() such that
such that ![]() , as shown in the following diagram:
, as shown in the following diagram:
Note that ![]() and
and ![]() . We thus have by AA Similarity that
. We thus have by AA Similarity that ![]() . Similarly,
. Similarly, ![]() . Therefore,
. Therefore, ![]() We can solve for
We can solve for ![]() and
and ![]() as follows:
as follows: ![]() Then the following sequence of equations holds:
Then the following sequence of equations holds: ![]() Multiplying this equation by
Multiplying this equation by ![]() yields the desired
yields the desired ![]() .
. ![]()
Proof 2: Inequalities
The well-known Trivial Inequality states that if ![]() is a real number, then
is a real number, then ![]() . Prove that if
. Prove that if ![]() and
and ![]() are nonnegative real numbers, then
are nonnegative real numbers, then ![]()
Explanation
I found the proof by working backwards; I started with the desired result, and connected it to something true. Here is the wall of equations on my page (sadly I can't get them aligned):
 Because the left-hand side of this equation is a perfect square, this is actually the Trivial Inequality in disguise. The desired inequality is therefore implied by a true result. We can now write a proof:
Because the left-hand side of this equation is a perfect square, this is actually the Trivial Inequality in disguise. The desired inequality is therefore implied by a true result. We can now write a proof:
Bad Proof
I start out with ![]() Multiply the inequality by
Multiply the inequality by ![]() and square it,
and square it, ![]() . Letting our algebra go on autopilot,
. Letting our algebra go on autopilot, ![]() and
and ![]() , so
, so ![]() . This is true by Trivial Inequality, which completes the proof.
. This is true by Trivial Inequality, which completes the proof. ![]()
Why is this proof bad?
- Written Backwards: We must always write proofs like: true result
 desired result. However, the proof is written backwards so that the desired result
desired result. However, the proof is written backwards so that the desired result  true result. The Trivial Inequality should be at the start, not the end.
true result. The Trivial Inequality should be at the start, not the end. - Informal Word Choice: Please don't use the phrase "algebra autopilot" in a proof, and don't write sentences with no verbs (see the "Multiply the inequality by
 and square it"). Also, don't use "I," although "we" is totally acceptable.
and square it"). Also, don't use "I," although "we" is totally acceptable. - Not Enough Space: A little more space would make this proof easier to read. Important equations should have their own line.
Good Proof 1
By the Trivial Inequality, we have that ![]() Factoring this inequality returns
Factoring this inequality returns ![]() . We add
. We add ![]() to both sides and factor to get
to both sides and factor to get ![]() . Note that because
. Note that because ![]() and
and ![]() are nonnegative, both sides are nonnegative; we may therefore take the square root of the inequality, which yields
are nonnegative, both sides are nonnegative; we may therefore take the square root of the inequality, which yields ![]() Finally, dividing both sides by
Finally, dividing both sides by ![]() gives
gives ![]() , which completes the proof.
, which completes the proof. ![]()
Good Proof 2
By the Trivial Inequality, we have that ![]() Then the following sequence of inequalities holds:
Then the following sequence of inequalities holds:
 Note that because
Note that because ![]() and
and ![]() are nonnegative, both sides of this final inequality are nonnegative; we may therefore take the square root of both sides, which yields
are nonnegative, both sides of this final inequality are nonnegative; we may therefore take the square root of both sides, which yields ![]() Finally, dividing the inequality by
Finally, dividing the inequality by ![]() gives
gives ![]() , which completes the proof.
, which completes the proof. ![]()