Sharygin Olympiads, the best
Igor Fedorovich Sharygin (13/02/1937 - 12/03/2004, Moscow) - Soviet and Russian mathematician and teacher, specialist in elementary geometry, popularizer of science. He wrote many textbooks on geometry and created a number of beautiful problems. He headed the mathematics section of the Russian Soros Olympiads. After his death, Russia annually hosts the Geometry Olympiad for high school students. It consists of two rounds – correspondence and final. The correspondence round lasts 3 months.
The best problems of these Olympiads will be published. The numbering contains the year of the Olympiad and the serial number of the problem. Solutions are often different from the original ones.
Contents
[hide]2024, Problem 23
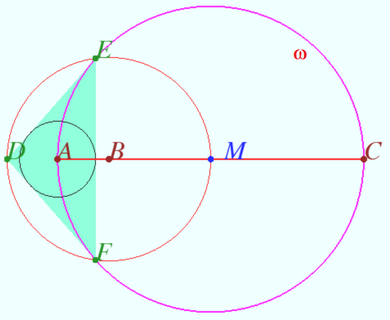
A point ![]() moves along a circle
moves along a circle ![]() Let
Let ![]() and
and ![]() be fixed points of
be fixed points of ![]() and
and ![]() be an arbitrary point inside
be an arbitrary point inside ![]()
The common external tangents to the circumcircles of triangles ![]() and
and ![]() meet at point
meet at point ![]()
Prove that all points ![]() lie on two fixed lines.
lie on two fixed lines.
Solution
Denote ![]()
![]()
![]() is the circumcenter of
is the circumcenter of ![]() is the circumcenter of
is the circumcenter of ![]()
Let ![]() and
and ![]() be the midpoints of the arcs
be the midpoints of the arcs ![]() of
of ![]()
Let ![]() and
and ![]() be the midpoints of the arcs
be the midpoints of the arcs ![]() of
of ![]()
These points not depends from position of point ![]()
Suppose, ![]() see diagram).
see diagram).
![]()
![]() Let
Let ![]()
![]() Similarly,
Similarly, ![]()
Let ![]()
Therefore ![]() Similarly, if
Similarly, if ![]() then
then ![]()
vladimir.shelomovskii@gmail.com, vvsss
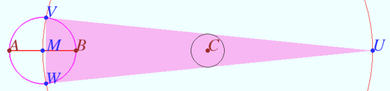
2024, Problem 22
A segment ![]() is given. Let
is given. Let ![]() be an arbitrary point of the perpendicular bisector to
be an arbitrary point of the perpendicular bisector to ![]() be the point on the circumcircle of
be the point on the circumcircle of ![]() opposite to
opposite to ![]() and an ellipse centered at
and an ellipse centered at ![]() touche
touche ![]()
Find the locus of touching points ![]() of the ellipse with the line
of the ellipse with the line ![]()
Solution
Denote ![]() the midpoint
the midpoint ![]() the point on the line
the point on the line ![]()
![]()
![]() In order to find the ordinate of point
In order to find the ordinate of point ![]() we perform an affine transformation (compression along axis
we perform an affine transformation (compression along axis ![]() which will transform the ellipse
which will transform the ellipse ![]() into a circle with diameter
into a circle with diameter ![]() The tangent of the
The tangent of the ![]() maps into the tangent of the
maps into the tangent of the ![]()
![]()
![]()
![]()
![]() Denote
Denote ![]()
So point ![]() is the fixed point (
is the fixed point (![]() not depends from angle
not depends from angle ![]()
Therefore point ![]() lies on the circle with diameter
lies on the circle with diameter ![]() (except points
(except points ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
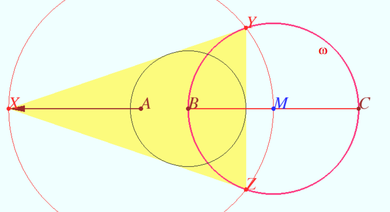
2024, Problem 21
A chord ![]() of the circumcircle of a triangle
of the circumcircle of a triangle ![]() meets the sides
meets the sides ![]() at points
at points ![]() respectively. The tangents to the circumcircle at
respectively. The tangents to the circumcircle at ![]() and
and ![]() meet at point
meet at point ![]() and the tangents at points
and the tangents at points ![]() and
and ![]() meets at point
meets at point ![]() The line
The line ![]() meets
meets ![]() at point
at point ![]()
Prove that the lines ![]() and
and ![]() concur.
concur.
Proof
WLOG, ![]() Denote
Denote ![]()
Point ![]() is inside
is inside ![]()
We use Pascal’s theorem for quadrilateral ![]() and get
and get ![]()
We use projective transformation which maps ![]() to a circle and that maps the point
to a circle and that maps the point ![]() to its center.
to its center.
From this point we use the same letters for the results of mapping. Therefore the segments ![]() and
and ![]() are the diameters of
are the diameters of ![]() is the midpoint
is the midpoint ![]()
![]()
preimage ![]() lies on preimage
lies on preimage ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 19
A triangle ![]() its circumcircle
its circumcircle ![]() , and its incenter
, and its incenter ![]() are drawn on the plane.
are drawn on the plane.
Construct the circumcenter ![]() of
of ![]() using only a ruler.
using only a ruler.
Solution
We successively construct:
- the midpoint ![]() of the arc
of the arc ![]()
- the midpoint ![]() of the arc
of the arc ![]()
- the polar ![]() of point
of point ![]()
- the polar ![]() of point
of point ![]()
- the polar ![]() of the line
of the line ![]()
- the tangent ![]() to
to ![]()
- the tangent ![]() to
to ![]()
- the trapezium ![]()
- the point ![]()
- the point ![]()
- the midpoint ![]() of the segment
of the segment ![]()
- the midpoint ![]() of the segment
of the segment ![]()
- the diameter ![]() of
of ![]()
- the diameter ![]() of
of ![]()
- the circumcenter ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 18
Let ![]() be the altitudes of an acute-angled triangle
be the altitudes of an acute-angled triangle ![]() be its excenter corresponding to
be its excenter corresponding to ![]() be the reflection of
be the reflection of ![]() about the line
about the line ![]() Points
Points ![]() are defined similarly. Prove that the lines
are defined similarly. Prove that the lines ![]() concur.
concur.
Proof
Denote ![]() the incenter of
the incenter of ![]() Points
Points ![]() are collinear.
We will prove that
are collinear.
We will prove that ![]() Denote
Denote ![]()
![]() - semiperimeter.
- semiperimeter.
![]() The area
The area ![]()
![]()
![]() Points
Points ![]() are collinear, so the lines
are collinear, so the lines ![]() concur at the point
concur at the point ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 16
Let ![]() and
and ![]() be the bisectors of a triangle
be the bisectors of a triangle ![]()
The segments ![]() and
and ![]() meet at point
meet at point ![]() Let
Let ![]() be the projection of
be the projection of ![]() to
to ![]()
Points ![]() and
and ![]() on the sides
on the sides ![]() and
and ![]() respectively, are such that
respectively, are such that ![]()
Prove that ![]()
Proof
![]() is the common side)
is the common side) ![]()
![]() is the midpoint
is the midpoint ![]()
![]() is the midpoint of
is the midpoint of ![]()
![]() (see Division of bisector for details.)
(see Division of bisector for details.)
So ![]() Denote
Denote ![]()
![]()
![]()
Another solution see 2024_Sharygin_olimpiad_Problem_16
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 12
The bisectors ![]() of a
of a ![]() with
with ![]() meet at point
meet at point ![]()
The circumcircles of triangles ![]() meet at point
meet at point ![]()
Prove that the line ![]() bisects the side
bisects the side ![]()
Proof
Denote ![]() the midpoint
the midpoint ![]()
![]()
![]() In triangles
In triangles ![]() and
and ![]() , by applying the law of sines, we get
, by applying the law of sines, we get
![]()
We use the formulas for circle ![]() and get
and get ![]()
![]() In triangles
In triangles ![]() and
and ![]() , by applying the law of sines, we get
, by applying the law of sines, we get
![]()
![]()
Therefore ![]() The function
The function ![]() increases monotonically on the interval
increases monotonically on the interval ![]()
This means ![]() and points
and points ![]() and
and ![]() are collinear.
are collinear.
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 9
Let ![]() be a trapezoid circumscribed around a circle
be a trapezoid circumscribed around a circle ![]() centered at
centered at ![]() which touches the sides
which touches the sides ![]() and
and ![]() at points
at points ![]() respectively.
respectively.
The line passing trough ![]() and parallel to the bases of trapezoid meets
and parallel to the bases of trapezoid meets ![]() at point
at point ![]()
Prove that ![]() and
and ![]() concur.
concur.
Solution
Solution 1. ![]()
![]()
![]() is the center of similarity of triangles
is the center of similarity of triangles ![]() and
and ![]()
Solution 2. ![]()
Denote ![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 8
Let ![]() be a quadrilateral with
be a quadrilateral with ![]() and
and ![]()
The incircle of ![]() touches the sides
touches the sides ![]() and
and ![]() at points
at points ![]() and
and ![]() respectively.
respectively.
The midpoints of segments ![]() and
and ![]() are points
are points ![]()
Prove that points ![]() are concyclic.
are concyclic.
Solution
![]()
![]()
![]() is the rotation of
is the rotation of ![]() around a point
around a point ![]() through an angle
through an angle ![]()
![]() is the rotation of
is the rotation of ![]() around a point
around a point ![]() through an angle
through an angle ![]()
So ![]() is the rotation of
is the rotation of ![]() around a point
around a point ![]() through an angle
through an angle ![]()
vladimir.shelomovskii@gmail.com, vvsss
2024, Problem 2
Three distinct collinear points are given. Construct the isosceles triangles such that these points are their circumcenter, incenter and excenter (in some order).
Solution
Let ![]() be the midpoint of the segment connecting the incenter and excenter. It is known that point
be the midpoint of the segment connecting the incenter and excenter. It is known that point ![]() belong the circumcircle.
Construction is possible if a circle with diameter IE (incenter – excenter) intersects a circle with radius OM (circumcenter – M). Situation when
belong the circumcircle.
Construction is possible if a circle with diameter IE (incenter – excenter) intersects a circle with radius OM (circumcenter – M). Situation when ![]() between
between ![]() and
and ![]() is impossible.
is impossible.
Denote points ![]() such that
such that ![]() and
and ![]()
Suppose point ![]() is circumcenter, so
is circumcenter, so ![]() is incenter.
is incenter. ![]() is midpoint BC. The vertices of the desired triangle are located at the intersection of a circle with center
is midpoint BC. The vertices of the desired triangle are located at the intersection of a circle with center ![]() and radius
and radius ![]() with
with ![]() and a line
and a line ![]()
Suppose point ![]() is circumcenter, so
is circumcenter, so ![]() is incenter.
is incenter. ![]() is midpoint
is midpoint ![]() The vertices of the desired triangle are located at the intersection of a circle with center
The vertices of the desired triangle are located at the intersection of a circle with center ![]() and radius
and radius ![]() with
with ![]() and a line
and a line ![]()
Suppose point ![]() is circumcenter, so
is circumcenter, so ![]() is incenter.
is incenter. ![]() is midpoint
is midpoint ![]() Suppose
Suppose ![]() The vertices of the desired triangle are located at the intersection of a circle with center
The vertices of the desired triangle are located at the intersection of a circle with center ![]() and radius
and radius ![]() with
with ![]() and a line
and a line ![]()
If ![]() there is not desired triangle.
there is not desired triangle.
vladimir.shelomovskii@gmail.com, vvsss