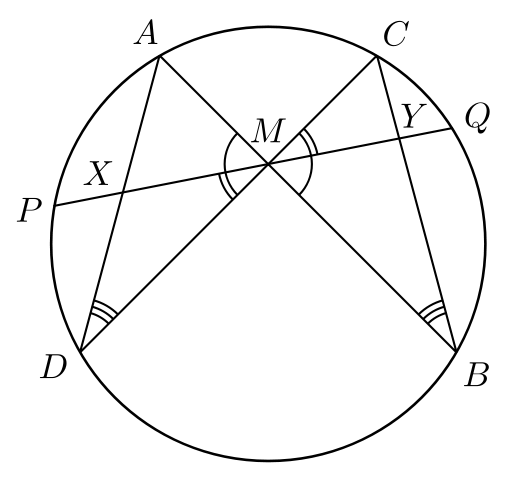
Butterfly Theorem
Let 
be the midpoint of chord 
of a circle, through which two other chords 
and 
are drawn. 
and 
intersect chord at 
and 
, respectively. The Butterfly Theorem states that is the midpoint of 
.
Proof
This simple proof uses projective geometry.
First we note that 
Therefore,
![\[\frac{(PX)(MQ)}{(PQ)(MX)} = \frac{(PM)(YQ)}{(PQ)(YM)}.\]](http://latex.artofproblemsolving.com/7/6/f/76f14d734cf4f6f44a177ce4a3e7f24c3fbf473b.png)
Since 
,
![\[\frac{MX}{YM} = \frac{XP}{QY}.\]](http://latex.artofproblemsolving.com/d/5/7/d57417825869128252443c99dc7976d36cc3c8a3.png)
Moreover,
![\[\frac{MX + PX}{YM + QY} = 1,\]](http://latex.artofproblemsolving.com/4/c/2/4c2977f9ff304e1aa22ec55c7a3b4fa11b6509d3.png)
so 
as desired.
.
Link to another proof :
http://agutie.homestead.com/FiLEs/GeometryButterfly.html
