2007 AIME I Problems/Problem 13
Problem
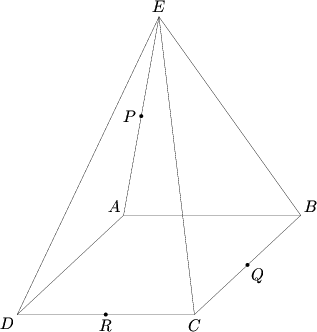
A square pyramid with base ![]() and vertex
and vertex ![]() has eight edges of length
has eight edges of length ![]() . A plane passes through the midpoints of
. A plane passes through the midpoints of ![]() ,
, ![]() , and
, and ![]() . The plane's intersection with the pyramid has an area that can be expressed as
. The plane's intersection with the pyramid has an area that can be expressed as ![]() . Find
. Find ![]() .
.
Contents[hide] |
import three; pointpen = black; pathpen = black+linewidth(0.7); currentprojection = perspective(2.5,-12,4);
triple A=(-2,2,0), B=(2,2,0), C=(2,-2,0), D=(-2,-2,0), E=(0,0,2*2^.5), P=(A+E)/2, Q=(B+C)/2, R=(C+D)/2;
D(A--B--C--D--A--E--B--E--C--E--D); MP("A",A); MP("B",B,(1,0,0)); MP("C",C); MP("D",D); MP("E",E,N); D(MP("P",P)); D(MP("Q",Q,(1,0,0))); D(MP("R",R));
(Error making remote request. Unknown error_msg)
|
Solution
Solution 1
Note first that the intersection is a pentagon.
Use 3D analytical geometry, setting the origin as the center of the square base and the pyramid’s points oriented as shown above. ![]() . Using the coordinates of the three points of intersection (
. Using the coordinates of the three points of intersection (![]() ), it is possible to determine the equation of the plane. The equation of a plane resembles
), it is possible to determine the equation of the plane. The equation of a plane resembles ![]() , and using the points we find that
, and using the points we find that ![]() ,
, ![]() , and
, and ![]() . It is then
. It is then ![]() .
.
import three; pointpen = black; pathpen = black+linewidth(0.7); currentprojection = perspective(2.5,-12,4);
triple A=(-2,2,0), B=(2,2,0), C=(2,-2,0), D=(-2,-2,0), E=(0,0,2*2^.5), P=(A+E)/2, Q=(B+C)/2, R=(C+D)/2, Y=(-3/2,-3/2,2^.5/2),X=(3/2,3/2,2^.5/2);
D(A--B--C--D--A--E--B--E--C--E--D); MP("A",A); MP("B",B,(1,0,0)); MP("C",C); MP("D",D); MP("E",E,N); D(MP("P",P)); D(MP("Q",Q,(1,0,0))); D(MP("R",R)); D(MP("Y",Y,NW)); D(MP("X",X,NE)); D(P--X--Q--R--Y--cycle,linetype("6 6")+linewidth(0.7));
(Error making remote request. Unknown error_msg) ![[asy]pointpen = black; pathpen = black+linewidth(0.7); pair P = (0, 2.5^.5), X = (3/2^.5,0), Y = (-3/2^.5,0), Q = (2^.5,-2.5^.5), R = (-2^.5,-2.5^.5); D(MP("P",P,N)--MP("X",X,NE)--MP("Q",Q)--MP("R",R)--MP("Y",Y,NW)--cycle); D(X--Y,linetype("6 6") + linewidth(0.7)); D(P--(0,-P.y),linetype("6 6") + linewidth(0.7)); MP("3\sqrt{2}",(X+Y)/2); MP("2\sqrt{2}",(Q+R)/2); MP("\sqrt{\frac{5}{2}}",(0,-P.y/2),E); MP("\sqrt{\frac{5}{2}}",(0,2*P.y/5),E); [/asy]](http://latex.artofproblemsolving.com/2/b/8/2b8b9e40ce0004d1e035b9700a3edf3a2deebbcc.png)
Write the equation of the lines and substitute to find that the other two points of intersection on ![]() ,
, ![]() are
are  . To find the area of the pentagon, break it up into pieces (an isosceles triangle on the top, an isosceles trapezoid on the bottom). Using the distance formula (
. To find the area of the pentagon, break it up into pieces (an isosceles triangle on the top, an isosceles trapezoid on the bottom). Using the distance formula (![]() ), it is possible to find that the area of the triangle is
), it is possible to find that the area of the triangle is ![]() . The trapezoid has area
. The trapezoid has area ![]() . In total, the area is
. In total, the area is ![]() , and the solution is
, and the solution is ![]() .
.
Solution 2
Use the same coordinate system as above, and let the plane determined by ![]() intersect
intersect ![]() at
at ![]() and
and ![]() at
at ![]() . Then the line
. Then the line ![]() is the intersection of the planes determined by
is the intersection of the planes determined by ![]() and
and ![]() .
.
Note that the plane determined by ![]() has the equation
has the equation ![]() , and
, and ![]() can be described by
can be described by ![]() . It intersects the plane when
. It intersects the plane when ![]() , or
, or ![]() . This intersection point has
. This intersection point has ![]() . Similarly, the intersection between
. Similarly, the intersection between ![]() and
and ![]() has
has ![]() . So
. So ![]() lies on the plane
lies on the plane ![]() , from which we obtain
, from which we obtain  and
and  . The area of the pentagon
. The area of the pentagon ![]() can be computed in the same way as above.
can be computed in the same way as above.
See also
| 2007 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()