Mock USAMO by probability1.01 dropped problems

Problem 1

Problem 2

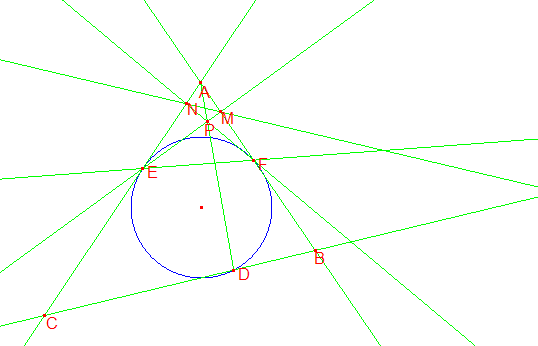
In triangle $ABC$ , $AB \not= AC$ , let the incircle touch $BC$ , $CA$ , and $AB$ at $D$ , $E$ , and $F$ respectively. Let $P$ be a point on $AD$ on the opposite side of $EF$ from $D$ . If $EP$ and $AB$ meet at $M$ , and $FP$ and $AC$ meet at $N$ , prove that $MN$ , $EF$ , and $BC$ concur. Reason: The whole incircle business seemed rather artificial. Besides, it wasn’t that difficult.