1985 AHSME Problems/Problem 14
Problem
Exactly three of the interior angles of a convex polygon are obtuse. What is the maximum number of sides of such a polygon?
![]()
Solution
Suppose that such a polygon has ![]() sides. Let the three obtuse angle measures, in degrees, be
sides. Let the three obtuse angle measures, in degrees, be ![]() ,
, ![]() , and
, and ![]() and the
and the ![]() acute angle measures, again in degrees, be
acute angle measures, again in degrees, be ![]() .
.
Since ![]() for each
for each ![]() , we have
, we have ![]() and similarly, since
and similarly, since ![]() for each
for each ![]() ,
, ![]() It follows that
It follows that ![]() and recalling that the sum of the interior angle measures of an
and recalling that the sum of the interior angle measures of an ![]() -gon is
-gon is ![]() , this reduces to
, this reduces to ![]() . Hence
. Hence ![]() so an upper bound is
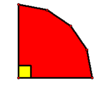
so an upper bound is ![]() , and it is easy to check that this bound can be attained by e.g. a convex hexagon with a right angle,
, and it is easy to check that this bound can be attained by e.g. a convex hexagon with a right angle, ![]() acute angles, and
acute angles, and ![]() obtuse angles, as shown below:
obtuse angles, as shown below:
Accordingly, the maximum possible number of sides of such a polygon is ![]() .
.
See Also
| 1985 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.