1989 AIME Problems/Problem 12
Problem
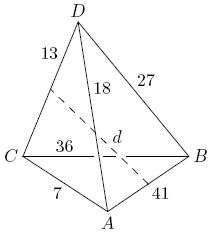
Let ![]() be a tetrahedron with
be a tetrahedron with ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , as shown in the figure. Let
, as shown in the figure. Let ![]() be the distance between the midpoints of edges
be the distance between the midpoints of edges ![]() and
and ![]() . Find
. Find ![]() .
.
Solution
Call the midpoint of ![]()
![]() and the midpoint of
and the midpoint of ![]()
![]() .
. ![]() is the median of triangle
is the median of triangle ![]() . The formula for the length of a median is
. The formula for the length of a median is ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are the side lengths of triangle, and
are the side lengths of triangle, and ![]() is the side that is bisected by median
is the side that is bisected by median ![]() . The formula is a direct result of the Law of Cosines applied twice with the angles formed by the median (Stewart's Theorem). We can also get this formula from the parallelogram law, that the sum of the squares of the diagonals is equal to the squares of the sides of a parallelogram (https://en.wikipedia.org/wiki/Parallelogram_law).
. The formula is a direct result of the Law of Cosines applied twice with the angles formed by the median (Stewart's Theorem). We can also get this formula from the parallelogram law, that the sum of the squares of the diagonals is equal to the squares of the sides of a parallelogram (https://en.wikipedia.org/wiki/Parallelogram_law).
We first find ![]() , which is the median of
, which is the median of ![]() .
.
![]()
Now we must find ![]() , which is the median of
, which is the median of ![]() .
.
![]()
Now that we know the sides of ![]() , we proceed to find the length of
, we proceed to find the length of ![]() .
.
![]()
See also
| 1989 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.