1989 AIME Problems/Problem 15
Contents
Problem
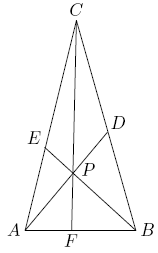
Point ![]() is inside
is inside ![]() . Line segments
. Line segments ![]() ,
, ![]() , and
, and ![]() are drawn with
are drawn with ![]() on
on ![]() ,
, ![]() on
on ![]() , and
, and ![]() on
on ![]() (see the figure below). Given that
(see the figure below). Given that ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , find the area of
, find the area of ![]() .
.
Solution
Solution 1
Because we're given three concurrent cevians and their lengths, it seems very tempting to apply Mass points. We immediately see that ![]() ,
, ![]() , and
, and ![]() . Now, we recall that the masses on the three sides of the triangle must be balanced out, so
. Now, we recall that the masses on the three sides of the triangle must be balanced out, so ![]() and
and ![]() . Thus,
. Thus, ![]() and
and ![]() .
.
Recalling that ![]() , we see that
, we see that ![]() and
and ![]() is a median to
is a median to ![]() in
in ![]() . Applying Stewart's Theorem,
. Applying Stewart's Theorem, ![]() , and
, and ![]() . Now notice that
. Now notice that ![]() , because both triangles share the same base and the
, because both triangles share the same base and the ![]() . Applying Heron's formula on triangle
. Applying Heron's formula on triangle ![]() with sides
with sides ![]() ,
, ![]() , and
, and ![]() ,
, ![]() and
and ![]() .
.
Solution 2
Using a different form of Ceva's Theorem, we have ![]()
Solving ![]() and
and ![]() , we obtain
, we obtain ![]() and
and ![]() .
.
Let ![]() be the point on
be the point on ![]() such that
such that ![]() .
Since
.
Since ![]() and
and ![]() ,
, ![]() . (Stewart's Theorem)
. (Stewart's Theorem)
Also, since ![]() and
and ![]() , we see that
, we see that ![]() ,
, ![]() , etc. (Stewart's Theorem)
Similarly, we have
, etc. (Stewart's Theorem)
Similarly, we have ![]() (
(![]() ) and thus
) and thus ![]() .
.
![]() is a
is a ![]() right triangle, so
right triangle, so ![]() (
(![]() ) is
) is ![]() .
Therefore, the area of
.
Therefore, the area of ![]() .
Using area ratio,
.
Using area ratio, ![]() .
.
Solution 3
Because the length of cevian ![]() is unknown, we can examine what happens when we extend it or decrease its length and see that it simply changes the angles between the cevians. Wouldn't it be great if it the length of
is unknown, we can examine what happens when we extend it or decrease its length and see that it simply changes the angles between the cevians. Wouldn't it be great if it the length of ![]() was such that
was such that ![]() ? Let's first assume it's a right angle and hope that everything works out.
? Let's first assume it's a right angle and hope that everything works out.
Extend ![]() to
to ![]() so that
so that ![]() . The result is that
. The result is that ![]() ,
, ![]() , and
, and ![]() because
because ![]() . Now we see that if we are able to show that
. Now we see that if we are able to show that ![]() , that is
, that is ![]() , then our right angle assumption will be true.
, then our right angle assumption will be true.
Apply the Pythagorean Theorem on ![]() to get
to get ![]() , so
, so ![]() and
and ![]() . Now, we apply the Law of Cosines on triangles
. Now, we apply the Law of Cosines on triangles ![]() and
and ![]() .
.
Let ![]() . Notice that
. Notice that ![]() and
and ![]() , so we get two nice equations.
, so we get two nice equations.
![]()
![]()
Solving, ![]() (yay!).
(yay!).
Now, the area is easy to find. ![]() .
.
[however, I think this solution is wrong, the A, B, and Cs do not match with the picture]
Solution 4
First, let ![]() and
and ![]() Thus, we can easily find that
Thus, we can easily find that ![]() Now,
Now, ![]() In the same manner, we find that
In the same manner, we find that ![]() Now, we can find that
Now, we can find that ![]() We can now use this to find that
We can now use this to find that ![]() Plugging this value in, we find that
Plugging this value in, we find that ![]() Now, since
Now, since ![]() we can find that
we can find that ![]() Setting
Setting ![]() we can apply Stewart's Theorem on triangle
we can apply Stewart's Theorem on triangle ![]() to find that
to find that ![]() Solving, we find that
Solving, we find that ![]() But,
But, ![]() meaning that
meaning that ![]() Since
Since ![]() we conclude that the answer is
we conclude that the answer is ![]() .
.
See also
| 1989 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Final Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.