1994 AIME Problems/Problem 14
Problem
A beam of light strikes ![]() at point
at point ![]() with angle of incidence
with angle of incidence ![]() and reflects with an equal angle of reflection as shown. The light beam continues its path, reflecting off line segments
and reflects with an equal angle of reflection as shown. The light beam continues its path, reflecting off line segments ![]() and
and ![]() according to the rule: angle of incidence equals angle of reflection. Given that
according to the rule: angle of incidence equals angle of reflection. Given that ![]() and
and ![]() determine the number of times the light beam will bounce off the two line segments. Include the first reflection at
determine the number of times the light beam will bounce off the two line segments. Include the first reflection at ![]() in your count.
in your count.
Solution
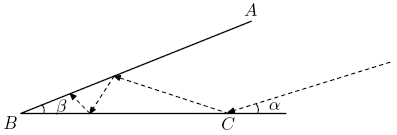
At each point of reflection, we pretend instead that the light continues to travel straight.
![[asy] pathpen = linewidth(0.7); size(250); real alpha = 28, beta = 36; pair B = MP("B",(0,0),NW), C = MP("C",D((1,0))), A = MP("A",expi(alpha * pi/180),N); path r = C + .4 * expi(beta * pi/180) -- C - 2*expi(beta * pi/180); D(A--B--(1.5,0));D(r);D(anglemark(C,B,D(A)));D(anglemark((1.5,0),C,C+.4*expi(beta*pi/180)));MP("\beta",B,(5,1.2),fontsize(9));MP("\alpha",C,(4,1.2),fontsize(9)); for(int i = 0; i < 180/alpha; ++i){ path l = B -- (1+i/2)*expi(-i * alpha * pi / 180); D(l, linetype("4 4")); D(IP(l,r)); } D(B); [/asy]](http://latex.artofproblemsolving.com/e/7/1/e718cb1b4bf8cc233b6061a4715b60c62a4b55ff.png) Note that after
Note that after ![]() reflections (excluding the first one at
reflections (excluding the first one at ![]() ) the extended line will form an angle
) the extended line will form an angle ![]() at point
at point ![]() . For the
. For the ![]() th reflection to be just inside or at point
th reflection to be just inside or at point ![]() , we must have
, we must have ![]() . Thus, our answer is, including the first intersection,
. Thus, our answer is, including the first intersection, ![]() .
.
See also
| 1994 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.