Difference between revisions of "1994 AIME Problems/Problem 2"
Pi is 3.14 (talk | contribs) (→Solution) |
|||
| (12 intermediate revisions by 10 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
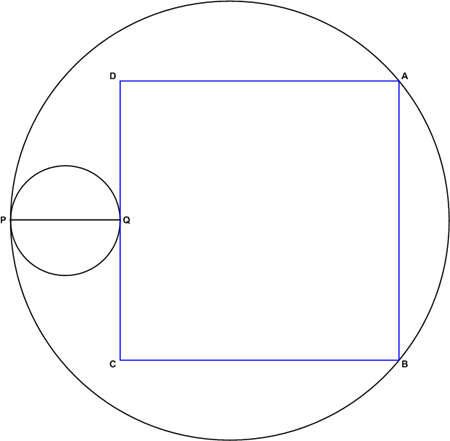
| + | A circle with diameter <math>\overline{PQ}</math> of length 10 is internally tangent at <math>P</math> to a circle of radius 20. Square <math>ABCD</math> is constructed with <math>A</math> and <math>B</math> on the larger circle, <math>\overline{CD}</math> tangent at <math>Q</math> to the smaller circle, and the smaller circle outside <math>ABCD</math>. The length of <math>\overline{AB}</math> can be written in the form <math>m + \sqrt{n}</math>, where <math>m</math> and <math>n</math> are integers. Find <math>m + n</math>. | ||
| + | |||
| + | [[Image:1994 AIME Problem 2.png]] | ||
| + | |||
| + | Note: The diagram was not given during the actual contest. | ||
== Solution == | == Solution == | ||
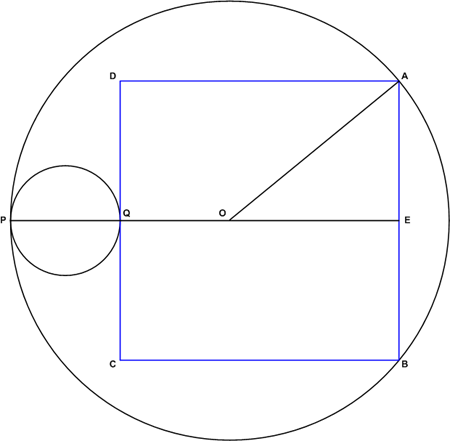
| + | [[Image:1994 AIME Problem 2 - Solution.png]] | ||
| + | |||
| + | Call the center of the larger circle <math>O</math>. Extend the diameter <math>\overline{PQ}</math> to the other side of the square (at point <math>E</math>), and draw <math>\overline{AO}</math>. We now have a [[right triangle]], with [[hypotenuse]] of length <math>20</math>. Since <math>OQ = OP - PQ = 20 - 10 = 10</math>, we know that <math>OE = AB - OQ = AB - 10</math>. The other leg, <math>AE</math>, is just <math>\frac 12 AB</math>. | ||
| + | |||
| + | Apply the [[Pythagorean Theorem]]: | ||
| + | |||
| + | :<math>(AB - 10)^2 + \left(\frac 12 AB\right)^2 = 20^2</math> | ||
| + | :<math>AB^2 - 20 AB + 100 + \frac 14 AB^2 - 400 = 0</math> | ||
| + | :<math>AB^2 - 16 AB - 240 = 0</math> | ||
| + | |||
| + | The [[quadratic formula]] shows that the answer is <math>\frac{16 \pm \sqrt{16^2 + 4 \cdot 240}}{2} = 8 \pm \sqrt{304}</math>. Discard the negative root, so our answer is <math>8 + 304 = \boxed{312}</math>. | ||
| + | |||
| + | == Video Solution by OmegaLearn == | ||
| + | https://youtu.be/nPVDavMoG9M?t=32 | ||
| + | |||
| + | ~ pi_is_3.14 | ||
== See also == | == See also == | ||
| − | + | {{AIME box|year=1994|num-b=1|num-a=3}} | |
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 03:53, 23 January 2023
Problem
A circle with diameter 
of length 10 is internally tangent at 
to a circle of radius 20. Square 
is constructed with 
and 
on the larger circle, 
tangent at 
to the smaller circle, and the smaller circle outside . The length of 
can be written in the form 
, where 
and 
are integers. Find 
.
Note: The diagram was not given during the actual contest.
Solution
Call the center of the larger circle 
. Extend the diameter to the other side of the square (at point 
), and draw 
. We now have a right triangle, with hypotenuse of length 
. Since 
, we know that 
. The other leg, 
, is just 
.
Apply the Pythagorean Theorem:
The quadratic formula shows that the answer is 
. Discard the negative root, so our answer is 
.
Video Solution by OmegaLearn
https://youtu.be/nPVDavMoG9M?t=32
~ pi_is_3.14
See also
| 1994 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 1 |
Followed by Problem 3 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
