1997 PMWC Problems
Contents
- 1 Problem I1
- 2 Problem I2
- 3 Problem I3
- 4 Problem I4
- 5 Problem I5
- 6 Problem I6
- 7 Problem I7
- 8 Problem I8
- 9 Problem I9
- 10 Problem I10
- 11 Problem I11
- 12 Problem I12
- 13 Problem I13
- 14 Problem I14
- 15 Problem I15
- 16 Problem T1
- 17 Problem T2
- 18 Problem T3
- 19 Problem T4
- 20 Problem T5
- 21 Problem T6
- 22 Problem T7
- 23 Problem T8
- 24 Problem T9
- 25 Problem T10
Problem I1
Evaluate ![]()
Problem I2
In the multiplication in the image, each letter and each box represent a single digit. Different letters represent different digits but a box can represent any digit. What does the five-digit number HAPPY stand for?
Problem I3
Peter is ill. He has to take medicine A every 8 hours, medicine B every 5 hours and medicine C every 10 hours. If he took all three medicines at 7 a.m. on Tuesday, when will he take them altogether again?
Problem I4
Each of the three diagrams in the image show a balance of weights using different objects. How many squares will balance a circle?
Problem I5
Two squares of different sizes overlap as shown in the given figure. What is the difference between the non-overlapping areas?
Problem I6
John and Mary went to a book shop and bought some exercise books. They had <dollar/>100 each. John could buy 7 large and 4 small ones. Mary could buy 5 large and 6 small ones and had <dollar/>5 left. How much was a small exercise book?
Problem I7
40% of girls and 50% of boys in a class got an 'A'. If there are only 12 students in the class who got 'A's and the ratio of boys and girls in the class is 45, how many students are there in the class?
Problem I8
![]()
Problem I9
A chemist mixed an acid of 48% concentration with the same acid of 80% concentration, and then added 2 litres of distilled water to the mixed acid. As a result, he got 10 litres of the acid of 40% concentration. How many millilitre of the acid of 48% concentration that the chemist had used? (1 litre = 1000 millilitres)
Problem I10
Mary took 24 chickens to the market. In the morning she
sold the chickens at ![]() 7 each and she only sold out less than
half of them. In the afternoon she discounted the price of
each chicken but the price was still an integral number in
dollar. In the afternoon she could sell all the chickens, and
she got totally
7 each and she only sold out less than
half of them. In the afternoon she discounted the price of
each chicken but the price was still an integral number in
dollar. In the afternoon she could sell all the chickens, and
she got totally ![]() 132 for the whole day. How many
chickens were sold in the morning?
132 for the whole day. How many
chickens were sold in the morning?
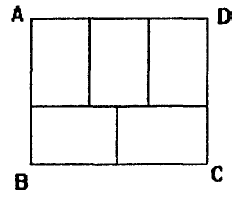
Problem I11
A rectangle ![]() is made up of five small congruent rectangles as shown in the given figure. Find the perimeter, in cm, of
is made up of five small congruent rectangles as shown in the given figure. Find the perimeter, in cm, of ![]() if its area is
if its area is ![]() .
.
Problem I12
In a die, 1 and 6,2 and 5,3 and 4 appear on opposite faces. When 2 dice are thrown, product of numbers appearing on the top and bottom faces of the 2 dice are formed as follows:
number on top face of 1st die x number on top face of 2nd die number on top face of 1st die x number on bottom face of 2nd die number on bottom face of 1st die x number on top face of 2nd die number on bottom face of 1st die x number on bottom face of 2nd die
What is the sum of these 4 products ?
Problem I13
A truck moved from A to B at a speed of ![]() km/h and returns from B to A at
km/h and returns from B to A at ![]() km/h. It traveled
km/h. It traveled ![]() rounds within 18 hours. What is the distance between A and B?
rounds within 18 hours. What is the distance between A and B?
Problem I14
If we make five two-digit numbers using the digits ![]() exactly once, and the product of the five numbers is maximized, find the greatest number among them.
exactly once, and the product of the five numbers is maximized, find the greatest number among them.
Problem I15
How many paths from A to B consist of exactly six line
segments (vertical, horizontal or inclined)?
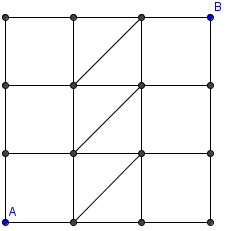
Problem T1
Problem T2
Evaluate
\begin{eqnarray*}
&& 1 \left(\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right) \\
&+& 3\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\\
&+&5\left(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\\
&+&7\left(\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\\
&+&9\left(\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)+11\left(\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\\
&+&13\left(\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)+15\left(\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}\right)\\
&+&17\left(\dfrac{1}{9}+\dfrac{1}{10}\right)+19\left(\dfrac{1}{10}\right) (Error compiling LaTeX. Unknown error_msg)
Problem T3
To type all the integers from 1 to 1997 using a typewriter on a piece of paper, how many does the key '9' needed to be pressed?
Problem T4
In one morning, a ferry traveled from Hong Kong to Kowloon and another ferry traveled from Kowloon to Hong Kong at a different speed. They started at the same time and met first time at 8:20. The two ferries then sailed to their destinations, stopped for 15 minutes and returned. The two ferries met again at 9:11. Suppose the two ferries traveled at a uniform speed throughout the whole journey, what time did the two ferries start their journey?
Problem T5
During recess, one of five pupils wrote something nasty on the chalkboard. When questioned by the class teacher, the following ensued:
'A': It was 'B' or 'C'
'B': Neither 'E' nor I did it.
'C': You are both lying.
'D': No, either A or B is telling the truth.
'E': No, 'D', that's not true.
The class teacher knows that three of them never lie while the other two cannot be trusted. Who was the culprit?
Problem T6
During a rebuilding project by contractors 'A', 'B' and 'C', there was a shortage of tractors. The contractors lent each other tractors as needed. At first, 'A' lent 'B' and 'C' as many tractors as they each already had. A few months later, 'B' lent 'A' and 'C' as many as they each already had. Still later, 'C' lent 'A' and 'B' as many as they each already had. By then each contractor had 24 tractors. How many tractors did each contractor originally have?
Problem T7
Color the surfaces of a cube of dimension 5*5*5 red, and then cur the cube into smaller cubes of dimension 1*1*1. Take out all the smaller cubes which have at least one red surface and fix a cuboid, keeping the surfaces of the cuboid red. Now what is the maximum possible volume of the cuboid?
Problem T8
Among the integers 1, 2, ..., 1997, what is the maximum number of integers that can be selected such that the sum of any two selected numbers is not a multiple of 7?
Problem T9
Find the two 10-digit numbers which become nine times as large if the order of the digits is reversed.
Problem T10
The twelve integers 1, 2, 3,..., 12 are arranged in a circle such that the difference of any two adjacent numbers is either 2, 3 or 4. What is the maximum number of the difference '4' can occur in any such arrangement?












