Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1998 AIME Problems/Problem 3"
(→‎Solution)
 
(3 intermediate revisions by 2 users not shown)
Line 3: Line 3:
  
 
== Solution ==
 
== Solution ==
 +
The equation given can be rewritten as:
 +
 
:<math>40|x| = - y^2 - 2xy + 400</math>
 
:<math>40|x| = - y^2 - 2xy + 400</math>
  
Line 12: Line 14:
 
Factoring the first one: (alternatively, it is also possible to [[completing the square|complete the square]])
 
Factoring the first one: (alternatively, it is also possible to [[completing the square|complete the square]])
  
−
:<math>40x + 2xy + = -y^2 + 400</math>
+
:<math>40x + 2xy  = -y^2 + 400</math>
 
:<math> 2x(20 + y)=  (20 - y)(20 + y)</math>
 
:<math> 2x(20 + y)=  (20 - y)(20 + y)</math>
  
Line 19: Line 21:
 
Hence, either <math>y = -20</math>, or <math>2x = 20 - y \Longrightarrow y = -2x + 20</math>.
 
Hence, either <math>y = -20</math>, or <math>2x = 20 - y \Longrightarrow y = -2x + 20</math>.
  
−
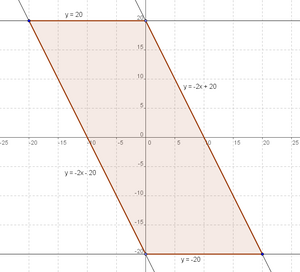
Similarily, for the second one, we get <math>y = 20</math> or <math> y = -2x - 20</math>. If we graph these four equations, we see that we get a parallelogram with base 20 and height 40. Hence the answer is <math>800</math>.
+
Similarily, for the second one, we get <math>y = 20</math> or <math> y = -2x - 20</math>. If we graph these four equations, we see that we get a parallelogram with base 20 and height 40. Hence the answer is <math>\boxed{800}</math>.
 +
 
 +
== Solution 2 ==
 +
The equation can be rewritten as: <math>(x+y)^2=(|x|-20)^2</math>. Do casework as above.
  
 
== See also ==
 
== See also ==

Latest revision as of 20:13, 23 February 2018

Problem

The graph of $y^2 + 2xy + 40|x|= 400$ partitions the plane into several regions. What is the area of the bounded region?

Solution

The equation given can be rewritten as:

$40|x| = - y^2 - 2xy + 400$

We can split the equation into a piecewise equation by breaking up the absolute value:

$40x = -y^2 - 2xy + 400\quad\quad x\ge 0$
$40x = y^2 + 2xy - 400 \quad \quad x < 0$

Factoring the first one: (alternatively, it is also possible to complete the square)

$40x + 2xy = -y^2 + 400$
$2x(20 + y)= (20 - y)(20 + y)$
AIME 1998-3.png

Hence, either $y = -20$, or $2x = 20 - y \Longrightarrow y = -2x + 20$.

Similarily, for the second one, we get $y = 20$ or $y = -2x - 20$. If we graph these four equations, we see that we get a parallelogram with base 20 and height 40. Hence the answer is $\boxed{800}$.

Solution 2

The equation can be rewritten as: $(x+y)^2=(|x|-20)^2$. Do casework as above.

See also

1998 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 2 		Followed by
Problem 4
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1998_AIME_Problems/Problem_3&oldid=92288"