Difference between revisions of "2007 AMC 10A Problems/Problem 15"
m (→Solution) |
|||
| Line 2: | Line 2: | ||
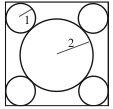
Four circles of radius <math>1</math> are each tangent to two sides of a square and externally tangent to a circle of radius <math>2</math>, as shown. What is the area of the square? | Four circles of radius <math>1</math> are each tangent to two sides of a square and externally tangent to a circle of radius <math>2</math>, as shown. What is the area of the square? | ||
| − | + | [[Image:2007 AMC 10A -15 for wiki.png]] | |
<math>\text{(A)}\ 32 \qquad \text{(B)}\ 22 + 12\sqrt {2}\qquad \text{(C)}\ 16 + 16\sqrt {3}\qquad \text{(D)}\ 48 \qquad \text{(E)}\ 36 + 16\sqrt {2}</math> | <math>\text{(A)}\ 32 \qquad \text{(B)}\ 22 + 12\sqrt {2}\qquad \text{(C)}\ 16 + 16\sqrt {3}\qquad \text{(D)}\ 48 \qquad \text{(E)}\ 36 + 16\sqrt {2}</math> | ||
==Solution== | ==Solution== | ||
| − | <math> | + | The diagonal has length <math>\sqrt{2}+1+2+2+1+\sqrt{2}=6+2\sqrt{2}</math>. Therefore the sides have length <math>2+3\sqrt{2}</math>, and the area is |
| − | {{ | + | <cmath>A=(2+3\sqrt{2})^2=4+6\sqrt{2}+6\sqrt{2}+18=22+12\sqrt{2} \Rightarrow \text{(C)}</cmath> |
==See Also== | ==See Also== | ||
Revision as of 19:01, 1 March 2008
Problem
Four circles of radius ![]() are each tangent to two sides of a square and externally tangent to a circle of radius
are each tangent to two sides of a square and externally tangent to a circle of radius ![]() , as shown. What is the area of the square?
, as shown. What is the area of the square?
![]()
Solution
The diagonal has length ![]() . Therefore the sides have length
. Therefore the sides have length ![]() , and the area is
, and the area is
![]()
See Also
| 2007 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Problem 16 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||