Difference between revisions of "2010 IMO Problems/Problem 2"
(formatted, added solution tag) |
(→See Also) |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 6: | Line 6: | ||
== Solution == | == Solution == | ||
| − | {{ | + | Note that it suffices to prove alternatively that if <math>EI</math> meets the circle again at <math>J</math> and <math>JD</math> meets <math>IF</math> at <math>G</math>, then <math>G</math> is the midpoint of <math>IF</math>. Let <math>JD</math> meet <math>BC</math> at <math>K</math>. |
| + | |||
| + | Observation 1. D is the midpoint of arc <math>BDC</math> because it lies on angle bisector <math>AI</math>. | ||
| + | |||
| + | Observation 2. <math>AI</math> bisects <math>\angle{FAE}</math> as well. | ||
| + | |||
| + | Key Lemma. Triangles <math>DKI</math> and <math>DIJ</math> are similar. | ||
| + | Proof. Because triangles <math>DKB</math> and <math>DBJ</math> are similar by AA Similarity (for <math>\angle{KBD}</math> and <math>\angle{BJD}</math> both intercept equally sized arcs), we have <math>BD^2 = BK \cdot BJ</math>. But we know that triangle <math>DBI</math> is isosceles (hint: prove <math>\angle{BID} = \angle{IBD}</math>), and so <math>BI^2 = BK \cdot BJ</math>. Hence, by SAS Similarity, triangles <math>DKI</math> and <math>DIJ</math> are similar, as desired. | ||
| + | |||
| + | Observation 3. As a result, we have <math>\angle{KID} = \angle{IJD} = \angle{DAE} = \angle{FAD}</math>. | ||
| + | |||
| + | Observation 4. <math>IK // AF</math>. | ||
| + | |||
| + | Observation 5. If <math>AF</math> and <math>JD</math> intersect at <math>L</math>, then <math>AJLI</math> is cyclic. | ||
| + | |||
| + | Observation 6. Because <math>\angle{ALI} = \angle{AJE} = \angle{AJC} + \angle{CJE} = \angle{B} + \angle{AEC} = \angle{B} + \angle{BAF} = \angle{AFC}</math>, we have <math>LI // FK</math>. | ||
| + | |||
| + | Observation 7. <math>LIKF</math> is a parallelogram, so its diagonals bisect each other, so <math>G</math> is the midpoint of <math>FI</math>, as desired. | ||
| + | |||
| + | ==Solution 2== | ||
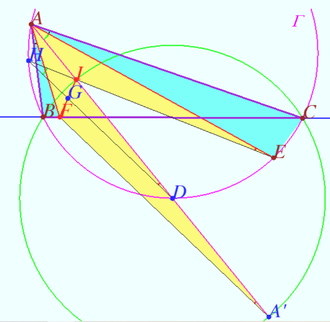
| + | [[File:2010 IMO 2.png|330px|right]] | ||
| + | Let <math>A'</math> be A-excenter <math>\triangle ABC \implies</math> | ||
| + | <cmath>DI = DB = DC = DA', AB \cdot AC = AI \cdot AA'.</cmath> | ||
| + | |||
| + | <cmath>\angle BAF = \angle EAC, \angle ABF = \angle ABC = \angle AEC \implies \triangle ABF \sim \triangle AEC \implies</cmath> | ||
| + | |||
| + | <cmath>\frac {AB}{AF} = \frac {AE}{AC} \implies AF \cdot AE = AB \cdot AC = AI \cdot AA' \implies \frac {AF}{AA'} = \frac {AI}{AE}.</cmath> | ||
| + | |||
| + | <cmath>\angle FAA' = \angle IAE \implies \triangle FAA' \sim \triangle IAE \implies \angle FA'A = \angle IEA.</cmath> | ||
| + | |||
| + | <cmath>IG = GF, ID = DA' \implies GD || FA' \implies \angle GDA = \angle FA'A = \angle IEA \implies </cmath> | ||
| + | the intersection of lines <math>EI</math> and <math>DG</math> lies on <math>\Gamma</math>. | ||
| + | |||
| + | After <i><b>pavel kozlov</b></i> '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
== See Also == | == See Also == | ||
{{IMO box|year=2010|num-b=1|num-a=3}} | {{IMO box|year=2010|num-b=1|num-a=3}} | ||
[[Category:Olympiad Geometry Problems]] | [[Category:Olympiad Geometry Problems]] | ||
Latest revision as of 14:52, 16 July 2023
Contents
Problem
Given a triangle ![]() , with
, with ![]() as its incenter and
as its incenter and ![]() as its circumcircle,
as its circumcircle, ![]() intersects
intersects ![]() again at
again at ![]() . Let
. Let ![]() be a point on arc
be a point on arc ![]() , and
, and ![]() a point on the segment
a point on the segment ![]() , such that
, such that ![]() . If
. If ![]() is the midpoint of
is the midpoint of ![]() , prove that the intersection of lines
, prove that the intersection of lines ![]() and
and ![]() lies on
lies on ![]() .
.
Authors: Tai Wai Ming and Wang Chongli, Hong Kong
Solution
Note that it suffices to prove alternatively that if ![]() meets the circle again at
meets the circle again at ![]() and
and ![]() meets
meets ![]() at
at ![]() , then
, then ![]() is the midpoint of
is the midpoint of ![]() . Let
. Let ![]() meet
meet ![]() at
at ![]() .
.
Observation 1. D is the midpoint of arc ![]() because it lies on angle bisector
because it lies on angle bisector ![]() .
.
Observation 2. ![]() bisects
bisects ![]() as well.
as well.
Key Lemma. Triangles ![]() and
and ![]() are similar.
Proof. Because triangles
are similar.
Proof. Because triangles ![]() and
and ![]() are similar by AA Similarity (for
are similar by AA Similarity (for ![]() and
and ![]() both intercept equally sized arcs), we have
both intercept equally sized arcs), we have ![]() . But we know that triangle
. But we know that triangle ![]() is isosceles (hint: prove
is isosceles (hint: prove ![]() ), and so
), and so ![]() . Hence, by SAS Similarity, triangles
. Hence, by SAS Similarity, triangles ![]() and
and ![]() are similar, as desired.
are similar, as desired.
Observation 3. As a result, we have ![]() .
.
Observation 4. ![]() .
.
Observation 5. If ![]() and
and ![]() intersect at
intersect at ![]() , then
, then ![]() is cyclic.
is cyclic.
Observation 6. Because ![]() , we have
, we have ![]() .
.
Observation 7. ![]() is a parallelogram, so its diagonals bisect each other, so
is a parallelogram, so its diagonals bisect each other, so ![]() is the midpoint of
is the midpoint of ![]() , as desired.
, as desired.
Solution 2
Let ![]() be A-excenter
be A-excenter ![]()
![]()
![]()
![]()
![]()
![]() the intersection of lines
the intersection of lines ![]() and
and ![]() lies on
lies on ![]() .
.
After pavel kozlov vladimir.shelomovskii@gmail.com, vvsss
See Also
| 2010 IMO (Problems) • Resources | ||
| Preceded by Problem 1 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 3 |
| All IMO Problems and Solutions | ||