Difference between revisions of "2011 AMC 10A Problems/Problem 24"
| Line 25: | Line 25: | ||
==Solution 3== | ==Solution 3== | ||
| − | Notice that the intersection of the tetrahedra is one of the bigger tetrahedra with the four smaller tetrahedra on its points cut off. Using the tetrahedron volume formula (<math>\frac{ | + | Notice that the intersection of the tetrahedra is one of the bigger tetrahedra with the four smaller tetrahedra on its points cut off. Using the tetrahedron volume formula (<math>\frac{\text{a}^3}{6\times\sqrt2}</math>), you get the volume of the intersection as <math>\frac{1}{3}-4\times\frac{1}{24}=\frac{1}{3}-\frac{1}{6}=\frac{1}{6}=\boxed{\text{(D)}}</math>. |
== See Also == | == See Also == | ||
Revision as of 01:20, 20 February 2019
Problem 24
Two distinct regular tetrahedra have all their vertices among the vertices of the same unit cube. What is the volume of the region formed by the intersection of the tetrahedra?
![]()
Diagram
The two tetrahedra look somewhat like this.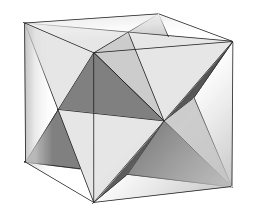
Solution 1
A regular unit tetrahedron can be split into eight tetrahedra that have lengths of ![]() .
The volume of a regular tetrahedron can be found using base area and height:
.
The volume of a regular tetrahedron can be found using base area and height:
For a tetrahedron of side length 1, its base area is ![]() , and its height can be found using Pythagoras' Theorem. Its height is
, and its height can be found using Pythagoras' Theorem. Its height is  . Its volume is
. Its volume is ![]() .
.
The tetrahedron actually has side length ![]() , so the actual volume is
, so the actual volume is ![]() .
.
On the eight small tetrahedra, the four tetrahedra on the corners of the large tetrahedra are not inside the other large tetrahedra. Thus, ![]() of the large tetrahedra will not be inside the other large tetrahedra.
of the large tetrahedra will not be inside the other large tetrahedra.
The intersection of the two tetrahedra is thus ![]() .
.
Solution 2
The intersection of the two tetrahedra is an octahedron that has points touching the center of each face of the original cube. We can split the octahedron into two square pyramids, and from there we can find the volume of each pyramid. The sides of the square face of the pyramid will have lengths of ![]() , so the volume of both pyramids (the whole octahedra) will be
, so the volume of both pyramids (the whole octahedra) will be  .
.
Solution 3
Notice that the intersection of the tetrahedra is one of the bigger tetrahedra with the four smaller tetrahedra on its points cut off. Using the tetrahedron volume formula (![]() ), you get the volume of the intersection as
), you get the volume of the intersection as ![]() .
.
See Also
| 2011 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 23 |
Followed by Problem 25 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









