2015 AIME I Problems/Problem 11
Contents
Problem
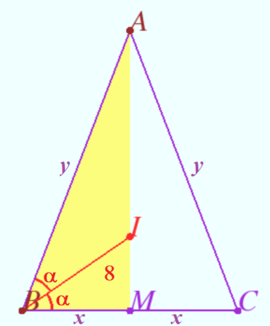
Triangle ![]() has positive integer side lengths with
has positive integer side lengths with ![]() . Let
. Let ![]() be the intersection of the bisectors of
be the intersection of the bisectors of ![]() and
and ![]() . Suppose
. Suppose ![]() . Find the smallest possible perimeter of
. Find the smallest possible perimeter of ![]() .
.
Solution 1
Let ![]() be the midpoint of
be the midpoint of ![]() . Then by SAS Congruence,
. Then by SAS Congruence, ![]() , so
, so ![]() .
.
Now let ![]() ,
, ![]() , and
, and ![]() .
.
Then ![]()
and ![]() .
.
Cross-multiplying yields ![]() .
.
Since ![]() ,
, ![]() must be positive, so
must be positive, so ![]() .
.
Additionally, since ![]() has hypotenuse
has hypotenuse ![]() of length
of length ![]() ,
, ![]() .
.
Therefore, given that ![]() is an integer, the only possible values for
is an integer, the only possible values for ![]() are
are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
However, only one of these values, ![]() , yields an integral value for
, yields an integral value for ![]() , so we conclude that
, so we conclude that ![]() and
and ![]() .
.
Thus the perimeter of ![]() must be
must be ![]() .
.
Solution 2 (No Trig)
Let ![]() and the foot of the altitude from
and the foot of the altitude from ![]() to
to ![]() be point
be point ![]() and
and ![]() . Since ABC is isosceles,
. Since ABC is isosceles, ![]() is on
is on ![]() . By Pythagorean Theorem,
. By Pythagorean Theorem, ![]() . Let
. Let ![]() and
and ![]() . By Angle Bisector theorem,
. By Angle Bisector theorem, ![]() . Also,
. Also, ![]() . Solving for
. Solving for ![]() , we get
, we get ![]() . Then, using Pythagorean Theorem on
. Then, using Pythagorean Theorem on ![]() we have
we have  . Simplifying, we have
. Simplifying, we have ![]() . Factoring out the
. Factoring out the ![]() , we have
, we have ![]() . Adding 1 to the fraction and simplifying, we have
. Adding 1 to the fraction and simplifying, we have ![]() . Crossing out the
. Crossing out the ![]() , and solving for
, and solving for ![]() yields
yields ![]() . Then, we continue as Solution 1 does.
. Then, we continue as Solution 1 does.
Solution 3
Let ![]() , call the midpoint of
, call the midpoint of ![]() point
point ![]() , call the point where the incircle meets
, call the point where the incircle meets ![]() point
point ![]() ,
,
and let ![]() . We are looking for the minimum value of
. We are looking for the minimum value of ![]() .
. ![]() is an altitude because the triangle
is an altitude because the triangle
is isosceles. By Pythagoras on ![]() , the inradius is
, the inradius is ![]() and by Pythagoras on
and by Pythagoras on ![]() ,
, ![]() is
is
![]() . By equal tangents,
. By equal tangents, ![]() , so
, so ![]() . Since
. Since ![]() is an inradius,
is an inradius, ![]() and
using pythagoras on
and
using pythagoras on ![]() yields
yields ![]()
![]() .
. ![]() is similar to
is similar to ![]() by
by ![]() , so we
, so we
can write ![]() . Simplifying,
. Simplifying, ![]() .
.
Squaring, subtracting 1 from both sides, and multiplying everything out, we get ![]() , which turns into
, which turns into ![]() . Finish as in Solution 1.
. Finish as in Solution 1.
Solution 4
Angle bisectors motivate trig bash.
Define angle ![]() . Foot of perpendicular from
. Foot of perpendicular from ![]() to
to ![]() is point
is point ![]() .
.
![]() , where
, where ![]() is an integer. Thus,
is an integer. Thus, ![]() . Via double angle, we calculate
. Via double angle, we calculate ![]() to be
to be ![]() . This is to be an integer. We can bound
. This is to be an integer. We can bound ![]() now, as
now, as ![]() to avoid negative values and
to avoid negative values and ![]() due to triangle inequality. Testing,
due to triangle inequality. Testing, ![]() works, giving
works, giving ![]() .
Our answer is
.
Our answer is ![]() .
- whatRthose
.
- whatRthose
Solution 5
Let ![]() be midpoint
be midpoint ![]()
![]() is the bisector of
is the bisector of ![]() in
in ![]()
![]()
![]()
![]() is integer,
is integer, ![]()
![]()
If ![]() then
then ![]() is not integer.
is not integer.
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Video Solution
https://youtu.be/R8kvayz7Rtw?si=hFg4yGZO4dxyxAuG
~MathProblemSolvingSkills.com
See Also
| 2015 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.