Difference between revisions of "2016 AIME I Problems/Problem 6"
(→Solution 7) |
m |
||
| (31 intermediate revisions by 13 users not shown) | |||
| Line 1: | Line 1: | ||
==Problem== | ==Problem== | ||
| − | In <math>\triangle ABC</math> let <math>I</math> be the center of the inscribed circle, and let the bisector of <math>\angle ACB</math> intersect <math>AB</math> at <math>L</math>. The line through <math>C</math> and <math>L</math> intersects the circumscribed circle of <math>\triangle ABC</math> at the two points <math>C</math> and <math>D</math>. If <math>LI=2</math> and <math>LD=3</math>, then <math>IC=\tfrac{ | + | In <math>\triangle ABC</math> let <math>I</math> be the center of the inscribed circle, and let the bisector of <math>\angle ACB</math> intersect <math>AB</math> at <math>L</math>. The line through <math>C</math> and <math>L</math> intersects the circumscribed circle of <math>\triangle ABC</math> at the two points <math>C</math> and <math>D</math>. If <math>LI=2</math> and <math>LD=3</math>, then <math>IC=\tfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>. |
| − | |||
==Solution 1== | ==Solution 1== | ||
Suppose we label the angles as shown below. | Suppose we label the angles as shown below. | ||
| Line 47: | Line 46: | ||
==Solution 4== | ==Solution 4== | ||
| − | Since <math>\angle{LAD} = \angle{BDC}</math> and <math>\angle{DLA}=\angle{ | + | Since <math>\angle{LAD} = \angle{BDC}</math> and <math>\angle{DLA}=\angle{DCB}</math>, <math>\triangle{DLA}\sim\triangle{DBC}</math>. Also, <math>\angle{DAC}=\angle{BLC}</math> and <math>\angle{ACD}=\angle{LCB}</math> so <math>\triangle{DAC}\sim\triangle{BLC}</math>. Now we can call <math>AC</math>, <math>b</math> and <math>BC</math>, <math>a</math>. By angle bisector theorem, <math>\frac{AD}{DB}=\frac{AC}{BC}</math>. So let <math>AD=bk</math> and <math>DB=ak</math> for some value of <math>k</math>. Now call <math>IC=x</math>. By the similar triangles we found earlier, <math>\frac{3}{ak}=\frac{bk}{x+2}</math> and <math>\frac{b}{x+5}=\frac{x+2}{a}</math>. We can simplify this to <math>abk^2=3x+6</math> and <math>ab=(x+5)(x+2)</math>. So we can plug the <math>ab</math> into the first equation and get <math>(x+5)(x+2)k^2=3(x+2) \rightarrow k^2(x+5)=3</math>. We can now draw a line through <math>A</math> and <math>I</math> that intersects <math>BC</math> at <math>E</math>. By mass points, we can assign a mass of <math>a</math> to <math>A</math>, <math>b</math> to <math>B</math>, and <math>a+b</math> to <math>D</math>. We can also assign a mass of <math>(a+b)k</math> to <math>C</math> by angle bisector theorem. So the ratio of <math>\frac{DI}{IC}=\frac{(a+b)k}{a+b}=k=\frac{2}{x}</math>. So since <math>k=\frac{2}{x}</math>, we can plug this back into the original equation to get <math>\left(\frac{2}{x}\right)^2(x+5)=3</math>. This means that <math>\frac{3x^2}{4}-x-5=0</math> which has roots -2 and <math>\frac{10}{3}</math> which means our <math>CI=\frac{10}{3}</math> and our answer is <math>\boxed{013}</math>. |
==Solution 5== | ==Solution 5== | ||
| Line 56: | Line 55: | ||
~Pluto1708 | ~Pluto1708 | ||
| − | Alternate solution: | + | Alternate solution: We can use the angle bisector theorem on <math>\triangle CBL</math> and bisector <math>BI</math> to get that <math>\tfrac{CI}{IL}=\tfrac{CI}{2}=\tfrac{BC}{BL}</math>. Since <math>\triangle CBL \sim \triangle ADL</math>, we get <math>\tfrac{BC}{BL}=\tfrac{AD}{DL}=\tfrac{5}{3}</math>. Thus, <math>CI=\tfrac{10}{3}</math> and <math>p+q=\boxed{13}</math>. |
(https://artofproblemsolving.com/community/c759169h1918283_geometry_problem) | (https://artofproblemsolving.com/community/c759169h1918283_geometry_problem) | ||
| − | == Solution 7 == | + | ==Solution 7== |
| + | We can just say that quadrilateral <math>ADBC</math> is a right kite with right angles at <math>A</math> and <math>B</math>. Let us construct another similar right kite with the points of tangency on <math>AC</math> and <math>BC</math> called <math>E</math> and <math>F</math> respectively, point <math>I</math>, and point <math>C</math>. Note that we only have to look at one half of the circle since the diagram is symmetrical. Let us call <math>CI</math> <math>x</math> for simplicity's sake. Based on the fact that <math>\triangle BCD</math> is similar to <math>\triangle FCI</math> we can use triangle proportionality to say that <math>BD</math> is <math>2\frac{x+5}{x}</math>. Using geometric mean theorem we can show that <math>BL</math> must be <math>\sqrt{3x+6}</math>. With Pythagorean Theorem we can say that <math>3x+6+9=4{(\frac{x+5}{x})}^2</math>. Multiplying both sides by <math>x^2</math> and moving everything to LHS will give you <math>3{x}^3+11{x}^2-40x-100=0</math> Since <math>x</math> must be in the form <math>\frac{p}{q}</math> we can assume that <math>x</math> is most likely a positive fraction in the form <math>\frac{p}{3}</math> where <math>p</math> is a factor of <math>100</math>. Testing the factors in synthetic division would lead <math>x = \frac{10}{3}</math>, giving us our desired answer <math>\boxed{013}</math>. ~Lopkiloinm | ||
| − | + | ==Solution 8 (Cyclic Quadrilaterals)== | |
| − | + | <asy> | |
| + | size(150); | ||
| + | import olympiad; | ||
| + | real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; | ||
| + | pair A=(0,0),B=(c,0),D=(c/2,-sqrt(25-(c/2)^2)); | ||
| + | pair C=intersectionpoints(circle(A,b),circle(B,a))[0]; | ||
| + | pair I=incenter(A,B,C); | ||
| + | pair L=extension(C,D,A,B); | ||
| + | dot(I^^A^^B^^C^^D); | ||
| + | draw(C--D); | ||
| + | path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} | ||
| + | draw(A--B--D--cycle); | ||
| + | draw(circumcircle(A,B,D)); | ||
| + | draw(A--C--B); | ||
| + | draw(A--I--B^^C--I); | ||
| + | draw(incircle(A,B,C)); | ||
| + | label("$A$",A,SW,fontsize(8)); | ||
| + | label("$B$",B,SE,fontsize(8)); | ||
| + | label("$C$",C,N,fontsize(8)); | ||
| + | label("$D$",D,S,fontsize(8)); | ||
| + | label("$I$",I,NE,fontsize(8)); | ||
| + | label("$L$",L,SW,fontsize(8)); | ||
| + | label("$\alpha$",A,5*dir(midangle(C,A,I)),fontsize(8)); | ||
| + | label("$\alpha$",A,5*dir(midangle(I,A,B)),fontsize(8)); | ||
| + | label("$\beta$",B,12*dir(midangle(A,B,I)),fontsize(8)); | ||
| + | label("$\beta$",B,12*dir(midangle(I,B,C)),fontsize(8)); | ||
| + | label("$\gamma$",C,5*dir(midangle(A,C,I)),fontsize(8)); | ||
| + | label("$\gamma$",C,5*dir(midangle(I,C,B)),fontsize(8)); | ||
| + | </asy> | ||
| + | Connect <math>D</math> to <math>A</math> and <math>D</math> to <math>B</math> to form quadrilateral <math>ACBD</math>. Since quadrilateral <math>ACBD</math> is cyclic, we can apply Ptolemy's Theorem on the quadrilateral. | ||
| + | |||
| + | Denote the length of <math>BD</math> and <math>AD</math> as <math>z</math> (they must be congruent, as <math>\angle ABD</math> and <math>\angle DAB</math> are both inscribed in arcs that have the same degree measure due to the angle bisector intersecting the circumcircle at <math>D</math>), and the lengths of <math>BC</math>, <math>AC</math>, <math>AB</math>, and <math>CI</math> as <math>a,b,c, x</math>, respectively. | ||
| + | |||
| + | After applying Ptolemy's, one will get that: | ||
| + | |||
| + | <cmath>z(a+b)=c(x+5)</cmath> | ||
| + | |||
| + | Next, since <math>ACBD</math> is cyclic, triangles <math>ALD</math> and <math>CLB</math> are similar, yielding the following equation once simplifications are made to the equation <math>\frac{AD}{CB}=\frac{AL}{BL}</math>, with the length of <math>BL</math> written in terms of <math>a,b,c</math> using the angle bisector theorem on triangle <math>ABC</math>: | ||
| + | |||
| + | <cmath>zc=3(a+b)</cmath> | ||
| + | |||
| + | Next, drawing in the bisector of <math>\angle BAC</math> to the incenter <math>I</math>, and applying the angle bisector theorem, we have that: | ||
| + | |||
| + | <cmath>cx=2(a+b)</cmath> | ||
| + | |||
| + | Now, solving for <math>z</math> in the second equation, and <math>x</math> in the third equation and plugging them both back into the first equation, and making the substitution <math>w=\frac{a+b}{c}</math>, we get the quadratic equation: | ||
| + | |||
| + | <cmath>3w^2-2w-5=0</cmath> | ||
| + | |||
| + | Solving, we get <math>w=5/3</math>, which gives <math>z=5</math> and <math>x=10/3</math>, when we rewrite the above equations in terms of <math>w</math>. Thus, our answer is <math>\boxed{013}</math> and we're done. | ||
| + | |||
| + | -mathislife52 | ||
| − | ( | + | ==Solution 9(Visual)== |
| + | [[File:2016 AIME I 6b.png|500px]] | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| − | + | ==Solution 10== | |
| + | Let <math>AB=c,BC=a,CA=b</math>, and <math>x=\tfrac{a+b}{c}</math>. Then, notice that <math>\tfrac{CI}{IL}=\tfrac{a+b}{c}=x</math>, so <math>CI=IL\cdot{}x=2x</math>. Also, by the incenter-excenter lemma, <math>AD=BD=ID=IL+LD=5</math>. Therefore, by Ptolemy's Theorem on cyclic quadrilateral <math>ABCD</math>, <math>5a+5b=c(2x+5)</math>, so <math>5\left(\tfrac{a+b}{c}\right)=2x+5</math>, so <math>5x=2x+5</math>. Solving, we get that <math>x=\tfrac{5}{3}</math>, so <math>CI=\tfrac{10}{3}</math> and the answer is <math>10+3=\boxed{013}</math>. | ||
| − | + | ==Solution 11== | |
| − | + | Perform a <math>\sqrt{bc}</math> Inversion followed by a reflection along the angle bisector of <math>\angle BCA</math>. | |
| − | |||
| − | |||
| − | + | It's well known that | |
| + | <cmath>AB \leftrightarrow \odot CBA \implies L \leftrightarrow D</cmath> | ||
| + | <cmath>I \leftrightarrow I_A</cmath> | ||
| + | where <math>I_A</math> is the <math>A-</math>excenter. | ||
| − | + | Also by Fact 5, <math>DI_A = 5</math>. | |
| − | + | So, | |
| − | + | <cmath>CL \cdot CD = CI \cdot CI_A</cmath> | |
| − | + | <cmath>\implies (CI + IL) \cdot (CI + ID) = (CI) \cdot (CI + II_A)</cmath> | |
| − | + | <cmath>\implies (CI + 2) \cdot (CI + 5) = (CI) \cdot (CI + 10)</cmath> | |
| + | <cmath>\implies 7CI +10= 10CI</cmath> | ||
| + | <cmath>\implies CI = \boxed{\dfrac{10}{3}}.\blacksquare</cmath> | ||
| − | + | ~kamatadu | |
| − | |||
| − | |||
| − | + | ==Solution 12== | |
| + | Without loss of generality, let <math>\triangle ABC</math> be isosceles. Note that by the incenter-excenter lemma, <math>DI = DA = DB.</math> Hence, <math>DA=DB=5.</math> Let the point of tangency of the incircle and <math>\overline{BC}</math> be <math>F</math> and the point of tangency of the incircle and <math>\overline{AC}</math> be <math>E.</math> We note that <math>\angle ALC = \angle BLC = 90^\circ</math> and <math>LA=LB=4,</math> which immediately gives <math>AE=BF=4.</math> Applying the Pythagorean Theorem on <math>\triangle ALC</math> and <math>\triangle IEC</math> gives <math>2^2+x^2=y^2</math> and <math>4^2+(2+y)^2 = (4+x)^2.</math> Solving for <math>y</math> gives us <math>y=\frac{10}{3}.</math> Therefore, <math>IC = \frac{10}{3}</math> so the answer is <math>\boxed{13}.</math> | ||
| − | + | ~peelybonehead | |
== See also == | == See also == | ||
{{AIME box|year=2016|n=I|num-b=5|num-a=7}} | {{AIME box|year=2016|n=I|num-b=5|num-a=7}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 20:04, 27 August 2023
Contents
Problem
In ![]() let
let ![]() be the center of the inscribed circle, and let the bisector of
be the center of the inscribed circle, and let the bisector of ![]() intersect
intersect ![]() at
at ![]() . The line through
. The line through ![]() and
and ![]() intersects the circumscribed circle of
intersects the circumscribed circle of ![]() at the two points
at the two points ![]() and
and ![]() . If
. If ![]() and
and ![]() , then
, then ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1
Suppose we label the angles as shown below.
![[asy] size(150); import olympiad; real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; pair A=(0,0),B=(c,0),D=(c/2,-sqrt(25-(c/2)^2)); pair C=intersectionpoints(circle(A,b),circle(B,a))[0]; pair I=incenter(A,B,C); pair L=extension(C,D,A,B); dot(I^^A^^B^^C^^D); draw(C--D); path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} draw(A--B--D--cycle); draw(circumcircle(A,B,D)); draw(A--C--B); draw(A--I--B^^C--I); draw(incircle(A,B,C)); label("$A$",A,SW,fontsize(8)); label("$B$",B,SE,fontsize(8)); label("$C$",C,N,fontsize(8)); label("$D$",D,S,fontsize(8)); label("$I$",I,NE,fontsize(8)); label("$L$",L,SW,fontsize(8)); label("$\alpha$",A,5*dir(midangle(C,A,I)),fontsize(8)); label("$\alpha$",A,5*dir(midangle(I,A,B)),fontsize(8)); label("$\beta$",B,12*dir(midangle(A,B,I)),fontsize(8)); label("$\beta$",B,12*dir(midangle(I,B,C)),fontsize(8)); label("$\gamma$",C,5*dir(midangle(A,C,I)),fontsize(8)); label("$\gamma$",C,5*dir(midangle(I,C,B)),fontsize(8)); [/asy]](http://latex.artofproblemsolving.com/5/6/c/56cc513300c04fd609c54fac8f20d478eb5950b4.png) As
As ![]() and
and ![]() intercept the same arc, we know that
intercept the same arc, we know that ![]() . Similarly,
. Similarly, ![]() . Also, using
. Also, using ![]() , we find
, we find ![]() . Therefore,
. Therefore, ![]() . Therefore,
. Therefore, ![]() , so
, so ![]() must be isosceles with
must be isosceles with ![]() . Similarly,
. Similarly, ![]() . Then
. Then ![]() , hence
, hence ![]() . Also,
. Also, ![]() bisects
bisects ![]() , so by the Angle Bisector Theorem
, so by the Angle Bisector Theorem ![]() . Thus
. Thus ![]() , and the answer is
, and the answer is ![]() .
.
Solution 2
WLOG assume ![]() is isosceles. Then,
is isosceles. Then, ![]() is the midpoint of
is the midpoint of ![]() , and
, and ![]() . Draw the perpendicular from
. Draw the perpendicular from ![]() to
to ![]() , and let it meet
, and let it meet ![]() at
at ![]() . Since
. Since ![]() ,
, ![]() is also
is also ![]() (they are both inradii). Set
(they are both inradii). Set ![]() as
as ![]() . Then, triangles
. Then, triangles ![]() and
and ![]() are similar, and
are similar, and ![]() . Thus,
. Thus, ![]() .
. ![]() , so
, so ![]() . Thus
. Thus ![]() . Solving for
. Solving for ![]() , we have:
, we have:
![]() , or
, or ![]() .
. ![]() is positive, so
is positive, so ![]() . As a result,
. As a result, ![]() and the answer is
and the answer is ![]()
Solution 3
WLOG assume ![]() is isosceles (with vertex
is isosceles (with vertex ![]() ). Let
). Let ![]() be the center of the circumcircle,
be the center of the circumcircle, ![]() the circumradius, and
the circumradius, and ![]() the inradius. A simple sketch will reveal that
the inradius. A simple sketch will reveal that ![]() must be obtuse (as an acute triangle will result in
must be obtuse (as an acute triangle will result in ![]() being greater than
being greater than ![]() ) and that
) and that ![]() and
and ![]() are collinear. Next, if
are collinear. Next, if ![]() ,
, ![]() and
and ![]() . Euler gives us that
. Euler gives us that ![]() , and in this case,
, and in this case, ![]() . Thus,
. Thus, ![]() . Solving for
. Solving for ![]() , we have
, we have ![]() , then
, then ![]() , yielding
, yielding ![]() . Next,
. Next, ![]() so
so ![]() . Finally,
. Finally, ![]() gives us
gives us ![]() , and
, and ![]() . Our answer is then
. Our answer is then ![]() .
.
Solution 4
Since ![]() and
and ![]() ,
, ![]() . Also,
. Also, ![]() and
and ![]() so
so ![]() . Now we can call
. Now we can call ![]() ,
, ![]() and
and ![]() ,
, ![]() . By angle bisector theorem,
. By angle bisector theorem, ![]() . So let
. So let ![]() and
and ![]() for some value of
for some value of ![]() . Now call
. Now call ![]() . By the similar triangles we found earlier,
. By the similar triangles we found earlier, ![]() and
and ![]() . We can simplify this to
. We can simplify this to ![]() and
and ![]() . So we can plug the
. So we can plug the ![]() into the first equation and get
into the first equation and get ![]() . We can now draw a line through
. We can now draw a line through ![]() and
and ![]() that intersects
that intersects ![]() at
at ![]() . By mass points, we can assign a mass of
. By mass points, we can assign a mass of ![]() to
to ![]() ,
, ![]() to
to ![]() , and
, and ![]() to
to ![]() . We can also assign a mass of
. We can also assign a mass of ![]() to
to ![]() by angle bisector theorem. So the ratio of
by angle bisector theorem. So the ratio of ![]() . So since
. So since ![]() , we can plug this back into the original equation to get
, we can plug this back into the original equation to get ![]() . This means that
. This means that ![]() which has roots -2 and
which has roots -2 and ![]() which means our
which means our ![]() and our answer is
and our answer is ![]() .
.
Solution 5
Since ![]() and
and ![]() both intercept arc
both intercept arc ![]() , it follows that
, it follows that ![]() . Note that
. Note that ![]() by the external angle theorem. It follows that
by the external angle theorem. It follows that ![]() , so we must have that
, so we must have that ![]() is isosceles, yielding
is isosceles, yielding ![]() . Note that
. Note that ![]() , so
, so ![]() . This yields
. This yields ![]() . It follows that
. It follows that ![]() , giving a final answer of
, giving a final answer of ![]() .
.
Solution 6
Let ![]() be the excenter opposite to
be the excenter opposite to ![]() in
in ![]() . By the incenter-excenter lemma
. By the incenter-excenter lemma ![]()
![]() . Its well known that
. Its well known that ![]() .
.![]() ~Pluto1708
~Pluto1708
Alternate solution: We can use the angle bisector theorem on ![]() and bisector
and bisector ![]() to get that
to get that ![]() . Since
. Since ![]() , we get
, we get ![]() . Thus,
. Thus, ![]() and
and ![]() .
(https://artofproblemsolving.com/community/c759169h1918283_geometry_problem)
.
(https://artofproblemsolving.com/community/c759169h1918283_geometry_problem)
Solution 7
We can just say that quadrilateral ![]() is a right kite with right angles at
is a right kite with right angles at ![]() and
and ![]() . Let us construct another similar right kite with the points of tangency on
. Let us construct another similar right kite with the points of tangency on ![]() and
and ![]() called
called ![]() and
and ![]() respectively, point
respectively, point ![]() , and point
, and point ![]() . Note that we only have to look at one half of the circle since the diagram is symmetrical. Let us call
. Note that we only have to look at one half of the circle since the diagram is symmetrical. Let us call ![]()
![]() for simplicity's sake. Based on the fact that
for simplicity's sake. Based on the fact that ![]() is similar to
is similar to ![]() we can use triangle proportionality to say that
we can use triangle proportionality to say that ![]() is
is ![]() . Using geometric mean theorem we can show that
. Using geometric mean theorem we can show that ![]() must be
must be ![]() . With Pythagorean Theorem we can say that
. With Pythagorean Theorem we can say that ![]() . Multiplying both sides by
. Multiplying both sides by ![]() and moving everything to LHS will give you
and moving everything to LHS will give you ![]() Since
Since ![]() must be in the form
must be in the form ![]() we can assume that
we can assume that ![]() is most likely a positive fraction in the form
is most likely a positive fraction in the form ![]() where
where ![]() is a factor of
is a factor of ![]() . Testing the factors in synthetic division would lead
. Testing the factors in synthetic division would lead ![]() , giving us our desired answer
, giving us our desired answer ![]() . ~Lopkiloinm
. ~Lopkiloinm
Solution 8 (Cyclic Quadrilaterals)
![[asy] size(150); import olympiad; real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; pair A=(0,0),B=(c,0),D=(c/2,-sqrt(25-(c/2)^2)); pair C=intersectionpoints(circle(A,b),circle(B,a))[0]; pair I=incenter(A,B,C); pair L=extension(C,D,A,B); dot(I^^A^^B^^C^^D); draw(C--D); path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} draw(A--B--D--cycle); draw(circumcircle(A,B,D)); draw(A--C--B); draw(A--I--B^^C--I); draw(incircle(A,B,C)); label("$A$",A,SW,fontsize(8)); label("$B$",B,SE,fontsize(8)); label("$C$",C,N,fontsize(8)); label("$D$",D,S,fontsize(8)); label("$I$",I,NE,fontsize(8)); label("$L$",L,SW,fontsize(8)); label("$\alpha$",A,5*dir(midangle(C,A,I)),fontsize(8)); label("$\alpha$",A,5*dir(midangle(I,A,B)),fontsize(8)); label("$\beta$",B,12*dir(midangle(A,B,I)),fontsize(8)); label("$\beta$",B,12*dir(midangle(I,B,C)),fontsize(8)); label("$\gamma$",C,5*dir(midangle(A,C,I)),fontsize(8)); label("$\gamma$",C,5*dir(midangle(I,C,B)),fontsize(8)); [/asy]](http://latex.artofproblemsolving.com/5/6/c/56cc513300c04fd609c54fac8f20d478eb5950b4.png) Connect
Connect ![]() to
to ![]() and
and ![]() to
to ![]() to form quadrilateral
to form quadrilateral ![]() . Since quadrilateral
. Since quadrilateral ![]() is cyclic, we can apply Ptolemy's Theorem on the quadrilateral.
is cyclic, we can apply Ptolemy's Theorem on the quadrilateral.
Denote the length of ![]() and
and ![]() as
as ![]() (they must be congruent, as
(they must be congruent, as ![]() and
and ![]() are both inscribed in arcs that have the same degree measure due to the angle bisector intersecting the circumcircle at
are both inscribed in arcs that have the same degree measure due to the angle bisector intersecting the circumcircle at ![]() ), and the lengths of
), and the lengths of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() as
as ![]() , respectively.
, respectively.
After applying Ptolemy's, one will get that:
![]()
Next, since ![]() is cyclic, triangles
is cyclic, triangles ![]() and
and ![]() are similar, yielding the following equation once simplifications are made to the equation
are similar, yielding the following equation once simplifications are made to the equation ![]() , with the length of
, with the length of ![]() written in terms of
written in terms of ![]() using the angle bisector theorem on triangle
using the angle bisector theorem on triangle ![]() :
:
![]()
Next, drawing in the bisector of ![]() to the incenter
to the incenter ![]() , and applying the angle bisector theorem, we have that:
, and applying the angle bisector theorem, we have that:
![]()
Now, solving for ![]() in the second equation, and
in the second equation, and ![]() in the third equation and plugging them both back into the first equation, and making the substitution
in the third equation and plugging them both back into the first equation, and making the substitution ![]() , we get the quadratic equation:
, we get the quadratic equation:
![]()
Solving, we get ![]() , which gives
, which gives ![]() and
and ![]() , when we rewrite the above equations in terms of
, when we rewrite the above equations in terms of ![]() . Thus, our answer is
. Thus, our answer is ![]() and we're done.
and we're done.
-mathislife52
Solution 9(Visual)
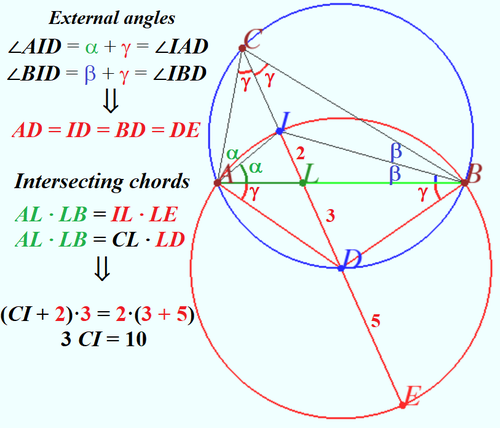 vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Solution 10
Let ![]() , and
, and ![]() . Then, notice that
. Then, notice that ![]() , so
, so ![]() . Also, by the incenter-excenter lemma,
. Also, by the incenter-excenter lemma, ![]() . Therefore, by Ptolemy's Theorem on cyclic quadrilateral
. Therefore, by Ptolemy's Theorem on cyclic quadrilateral ![]() ,
, ![]() , so
, so ![]() , so
, so ![]() . Solving, we get that
. Solving, we get that ![]() , so
, so ![]() and the answer is
and the answer is ![]() .
.
Solution 11
Perform a ![]() Inversion followed by a reflection along the angle bisector of
Inversion followed by a reflection along the angle bisector of ![]() .
.
It's well known that
![]()
![]() where
where ![]() is the
is the ![]() excenter.
excenter.
Also by Fact 5, ![]() .
.
So,
![]()
![]()
![]()
![]()
![]()
~kamatadu
Solution 12
Without loss of generality, let ![]() be isosceles. Note that by the incenter-excenter lemma,
be isosceles. Note that by the incenter-excenter lemma, ![]() Hence,
Hence, ![]() Let the point of tangency of the incircle and
Let the point of tangency of the incircle and ![]() be
be ![]() and the point of tangency of the incircle and
and the point of tangency of the incircle and ![]() be
be ![]() We note that
We note that ![]() and
and ![]() which immediately gives
which immediately gives ![]() Applying the Pythagorean Theorem on
Applying the Pythagorean Theorem on ![]() and
and ![]() gives
gives ![]() and
and ![]() Solving for
Solving for ![]() gives us
gives us ![]() Therefore,
Therefore, ![]() so the answer is
so the answer is ![]()
~peelybonehead
See also
| 2016 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









