Difference between revisions of "2018 AIME I Problems/Problem 13"
(→Solution 3a) |
(→Solution 3a) |
||
| Line 89: | Line 89: | ||
Using diagrams, we can recall known facts and using those facts for making sequence of equations. | Using diagrams, we can recall known facts and using those facts for making sequence of equations. | ||
| − | + | <cmath>\frac {(r-r_1)\cdot (r-r_2)}{r_1 \cdot r_2} =\tan\beta \tan\gamma.</cmath> | |
The twice area of <math>\triangle ABC</math> is | The twice area of <math>\triangle ABC</math> is | ||
| Line 99: | Line 99: | ||
[[File:2018 AIME I 13g.png|350px|right]] | [[File:2018 AIME I 13g.png|350px|right]] | ||
| − | [[File:2018 AIME I 13d.png| | + | [[File:2018 AIME I 13d.png|400px]] |
| − | [[File:2018 AIME I 13f.png| | + | [[File:2018 AIME I 13f.png|350px]] |
'''Shelomovskii, vvsss, www.deoma-cmd.ru''' | '''Shelomovskii, vvsss, www.deoma-cmd.ru''' | ||
Revision as of 15:51, 26 June 2022
Contents
Problem
Let ![]() have side lengths
have side lengths ![]() ,
, ![]() , and
, and ![]() . Point
. Point ![]() lies in the interior of
lies in the interior of ![]() , and points
, and points ![]() and
and ![]() are the incenters of
are the incenters of ![]() and
and ![]() , respectively. Find the minimum possible area of
, respectively. Find the minimum possible area of ![]() as
as ![]() varies along
varies along ![]() .
.
Solution 1 (Official MAA)
First note that ![]() is a constant not depending on
is a constant not depending on ![]() , so by
, so by ![]() it suffices to minimize
it suffices to minimize ![]() . Let
. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Remark that
. Remark that ![]() Applying the Law of Sines to
Applying the Law of Sines to ![]() gives
gives ![]() Analogously one can derive
Analogously one can derive ![]() , and so
, and so ![]() with equality when
with equality when ![]() , that is, when
, that is, when ![]() is the foot of the perpendicular from
is the foot of the perpendicular from ![]() to
to ![]() . In this case the desired area is
. In this case the desired area is ![]() . To make this feasible to compute, note that
. To make this feasible to compute, note that ![\[\sin\frac A2=\sqrt{\frac{1-\cos A}2}=\sqrt{\frac{1-\frac{b^2+c^2-a^2}{2bc}}2} = \sqrt{\dfrac{(a-b+c)(a+b-c)}{4bc}}.\]](http://latex.artofproblemsolving.com/6/9/7/697053dfbaa5f36e17c51a597f420e04697c805b.png) Applying similar logic to
Applying similar logic to ![]() and
and ![]() and simplifying yields a final answer of
and simplifying yields a final answer of 
Solution 2 (A lengthier, but less trigonometric approach)
First, instead of using angles to find ![]() , let's try to find the area of other, simpler figures, and subtract that from
, let's try to find the area of other, simpler figures, and subtract that from ![]() . However, to do this, we need to be able to figure out the length of the inradii, and so, we need to find
. However, to do this, we need to be able to figure out the length of the inradii, and so, we need to find ![]() .
.
To minimize ![]() , intuitively, we should try to minimize the length of
, intuitively, we should try to minimize the length of ![]() , since, after using the
, since, after using the ![]() formula for the area of a triangle, we'll be able to minimize the inradii lengths, and thus, eventually minimize the area of
formula for the area of a triangle, we'll be able to minimize the inradii lengths, and thus, eventually minimize the area of ![]() . (Proof needed here).
. (Proof needed here).
We need to minimize ![]() . Let
. Let ![]() ,
, ![]() , and
, and ![]() . After an application of Stewart's Theorem, we will get that
. After an application of Stewart's Theorem, we will get that ![]() To minimize this quadratic,
To minimize this quadratic, ![]() whereby we conclude that
whereby we conclude that ![]() .
.
From here, draw perpendiculars down from ![]() and
and ![]() to
to ![]() and
and ![]() respectively, and label the foot of these perpendiculars
respectively, and label the foot of these perpendiculars ![]() and
and ![]() respectively. After, draw the inradii from
respectively. After, draw the inradii from ![]() to
to ![]() , and from
, and from ![]() to
to ![]() , and draw in
, and draw in ![]() .
.
Label the foot of the inradii to ![]() and
and ![]() ,
, ![]() and
and ![]() , respectively. From here, we see that to find
, respectively. From here, we see that to find ![]() , we need to find
, we need to find ![]() , and subtract off the sum of
, and subtract off the sum of ![]() and
and ![]() .
.
![]() can be found by finding the area of two quadrilaterals
can be found by finding the area of two quadrilaterals ![]() as well as the area of a trapezoid
as well as the area of a trapezoid ![]() . If we let the inradius of
. If we let the inradius of ![]() be
be ![]() and if we let the inradius of
and if we let the inradius of ![]() be
be ![]() , we'll find, after an application of basic geometry and careful calculations on paper, that
, we'll find, after an application of basic geometry and careful calculations on paper, that ![]() .
.
The area of two triangles can be found in a similar fashion, however, we must use ![]() substitution to solve for
substitution to solve for ![]() as well as
as well as ![]() . After doing this, we'll get a similar sum in terms of
. After doing this, we'll get a similar sum in terms of ![]() and
and ![]() for the area of those two triangles which is equal to
for the area of those two triangles which is equal to ![]()
Now we're set. Summing up the area of the Hexagon and the two triangles and simplifying, we get that the formula for ![]() is just
is just ![\[[ABC]-\left(\frac{(35+3\sqrt{21})(r_1)}{2}+\frac{(45+3r_2\sqrt{21})(r_2)}{2}\right).\]](http://latex.artofproblemsolving.com/e/d/7/ed75de39d2544c5acbbad80d0d2c955f3e141ce6.png)
Using Heron's formula, ![]() . Solving for
. Solving for ![]() and
and ![]() using Heron's in
using Heron's in ![]() and
and ![]() , we get that
, we get that ![]() and
and ![]() . From here, we just have to plug into our above equation and solve.
. From here, we just have to plug into our above equation and solve.
Doing so gets us that the minimum area of ![]()
-Azeem H.(Mathislife52) ~edited by phoenixfire
Video Solution by Osman Nal
https://www.youtube.com/watch?v=sT-wxV2rYqs
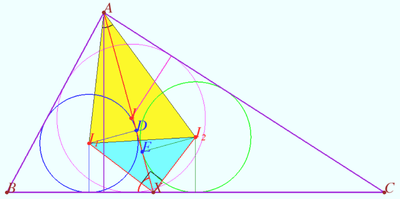
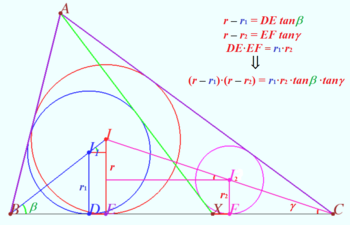
Solution 3 (Geometry only)
Let ![]() be semiperimeter of
be semiperimeter of ![]() be the height of
be the height of ![]() dropped from
dropped from ![]()
Let ![]() be inradius of the
be inradius of the ![]() and
and ![]() respectively.
respectively.
Using the Lemma (below), we get the area
![]()
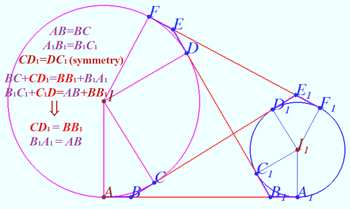
![]() Lemma
Lemma
![]()
Proof
![]() WLOG
WLOG ![]()
![]()
![]()
![]() if and only if
if and only if
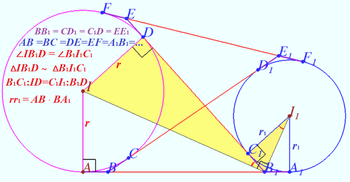
Claim
![]() Proof
Proof
Let ![]()
![]()
![]()
![]()
![]()
![]()
![]() We use Cosine Law for
We use Cosine Law for ![]() and
and ![]() and get
and get
![]() Last is evident, the claim has been proven.
Last is evident, the claim has been proven.
Shelomovskii, vvsss, www.deoma-cmd.ru
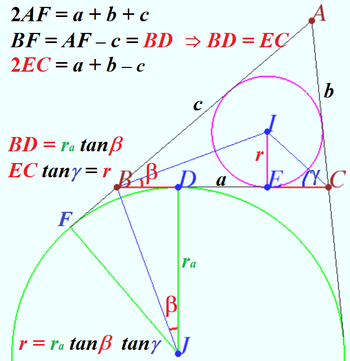
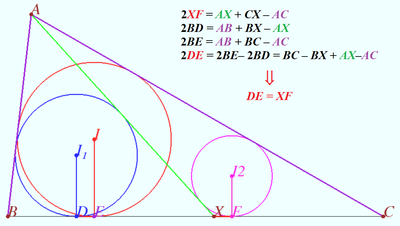
Solution 3a
Geometry proof of the equation ![]()
![]()
Using diagrams, we can recall known facts and using those facts for making sequence of equations.
![]()
The twice area of ![]() is
is
![]()
![]()
Therefore ![]()
Shelomovskii, vvsss, www.deoma-cmd.ru
See Also
| 2018 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.