Difference between revisions of "2019 IMO Problems/Problem 2"

Revision as of 12:15, 13 August 2022

In triangle $ABC$ , point $A_1$ lies on side $BC$ and point $B_1$ lies on side $AC$ . Let $P$ and $Q$ be points on segments $AA_1$ and $BB_1$ , respectively, such that $PQ$ is parallel to $AB$ . Let $P_1$ be a point on line $PB_1$ , such that $B_1$ lies strictly between $P$ and $P_1$ , and $\angle PP_1C=\angle BAC$ . Similarly, let $Q_1$ be the point on line $QA_1$ , such that $A_1$ lies strictly between $Q$ and $Q_1$ , and $\angle CQ_1Q=\angle CBA$ .

Prove that points $P,Q,P_1$ , and $Q_1$ are concyclic.

Solution

The essence of the proof is to build a circle through the points $P, Q,$ and two additional points $A_0$ and $B_0,$ then we prove that the points $P_1$ and $Q_1$ lie on the same circle.

Let the circumcircle of $\triangle ABC$ be $\Omega$ . Let $A_0$ and $B_0$ be the points of intersection of $AP$ and $BQ$ with $\Omega$ . Let $\angle BAP = \delta.$

$PQ||AB \implies \angle QPA_0 = \delta.$

$\angle BAP = \angle BB_0A_0 = \delta$ since they intersept the arc $BA_0$ of the circle $\Omega$ .

$\angle QPA_0 = \angle QB_0A_0 \implies QPB_0A_0$ is cyclic (in circle $\omega.$ )

Let $\angle BAC = \alpha, \angle AA_0B_0 = \varphi.$

$\angle PP_1C = \alpha, \angle BB_0C = \alpha$ since they intersept the arc $BC$ of the circle $\Omega.$ So $B_0P_1CB_1$ is cyclic.

$\angle ACB_0 = \angle AA_0B_0 = \varphi$ (since they intersept the arc $A_0B_0$ of the circle $\Omega.$

$\angle B_1CB_0 = \varphi.$ $\angle B_1P_1B_0 = \angle B_1CB_0 = \varphi$ (since they intersept the arc $B_1B_0$ of the circle $B_0P_1CB_1).$

Hence $\angle PA_0B_0 = \angle PP_1B_0 = \varphi,$ the point $P_1$ lies on $\omega.$

Similarly, point $Q_1$ lies on $\omega.$

vladimir.shelomovskii@gmail.com, vvsss, www.deoma–cmd.ru

@@ Line 4: / Line 4: @@
 ==Solution==
-[[File:2019 IMO 2.png|500px|right]]
+[[File:2019 IMO 2.png|440px|right]]
+[[File:2019 IMO 2a.png|440px|right]]
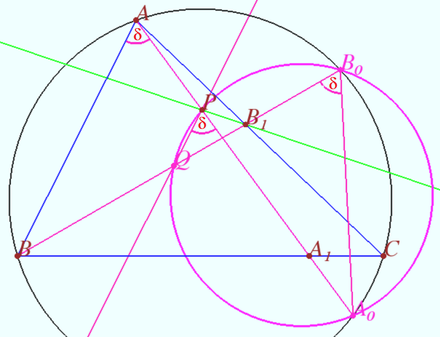
 The essence of the proof is to build a circle through the points <math>P, Q,</math> and two additional points <math>A_0</math> and <math>B_0,</math> then we prove that the points <math>P_1</math> and <math>Q_1</math> lie on the same circle.
@@ Line 14: / Line 15: @@
 <math>\angle QPA_0 = \angle QB_0A_0 \implies QPB_0A_0</math> is cyclic (in circle <math>\omega.</math>)
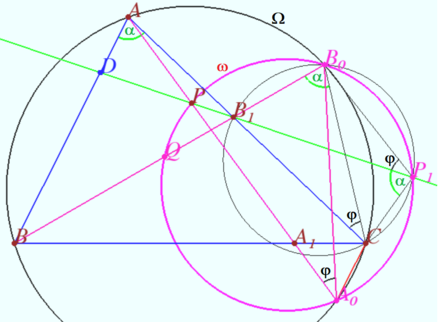
+Let <math>\angle BAC = \alpha, \angle AA_0B_0 = \varphi.</math>
+<math>\angle PP_1C = \alpha, \angle BB_0C = \alpha</math> since they intersept the arc <math>BC</math> of the circle <math>\Omega.</math>
+So <math>B_0P_1CB_1</math> is cyclic.
+<math>\angle ACB_0 = \angle AA_0B_0 =  \varphi</math> (since they intersept the arc <math>A_0B_0</math> of the circle  <math>\Omega.</math>
+<math>\angle B_1CB_0 = \varphi.</math>
+<math>\angle B_1P_1B_0 = \angle B_1CB_0 =  \varphi</math> (since they intersept the arc <math>B_1B_0</math> of the circle <math>B_0P_1CB_1).</math>
+Hence <math>\angle PA_0B_0 = \angle PP_1B_0 = \varphi,</math>  the point <math>P_1</math> lies on <math>\omega.</math>
+Similarly, point <math>Q_1</math> lies on  <math>\omega.</math>
+'''vladimir.shelomovskii@gmail.com, vvsss, www.deoma–cmd.ru'''

Page

Toolbox

Search

Difference between revisions of "2019 IMO Problems/Problem 2"

Revision as of 12:15, 13 August 2022

Solution