Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2019 USAMO Problems/Problem 2"

(→‎Solution 2)
(→‎Solution)
 
(4 intermediate revisions by the same user not shown)
Line 30: Line 30:
  
 
Since <math>P</math> is the isogonal conjugate of <math>N</math>, <math>\measuredangle PEA = \measuredangle MEC = \measuredangle BEN</math>. However <math>\measuredangle MEC = \measuredangle BEN</math> implies that <math>M</math> is the midpoint of <math>CD</math> from similar triangles, so we are done. <math>\square</math>
 
Since <math>P</math> is the isogonal conjugate of <math>N</math>, <math>\measuredangle PEA = \measuredangle MEC = \measuredangle BEN</math>. However <math>\measuredangle MEC = \measuredangle BEN</math> implies that <math>M</math> is the midpoint of <math>CD</math> from similar triangles, so we are done. <math>\square</math>
−
 
−
{{MAA Notice}}
 
  
 
==Solution 2==
 
==Solution 2==
Line 37: Line 35:
 
[[File:2019 USAMO 2a.png|450px|right]]
 
[[File:2019 USAMO 2a.png|450px|right]]
 
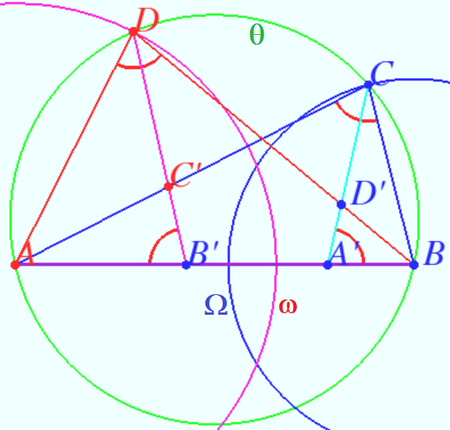
Let <math>\omega</math> be the circle centered at <math>A</math> with radius <math>AD.</math>
 
Let <math>\omega</math> be the circle centered at <math>A</math> with radius <math>AD.</math>
 +
 
Let <math>\Omega</math> be the circle centered at <math>B</math> with radius <math>BC.</math>
 
Let <math>\Omega</math> be the circle centered at <math>B</math> with radius <math>BC.</math>
−
We denote <math>I_\omega</math> and <math>I\Omega</math> inversion with respect to <math>\omega</math> and <math>\Omega,</math> respectively.
+
 
 +
We denote <math>I_\omega</math> and <math>I_\Omega</math> inversion with respect to <math>\omega</math> and <math>\Omega,</math> respectively.
 
<cmath>B'= I_\omega (B), C'= I_\omega (C), D = I_\omega (D) \implies</cmath>
 
<cmath>B'= I_\omega (B), C'= I_\omega (C), D = I_\omega (D) \implies</cmath>
 
<cmath>AB' \cdot AB = AD^2,  \angle ACB = \angle AB'C'.</cmath>
 
<cmath>AB' \cdot AB = AD^2,  \angle ACB = \angle AB'C'.</cmath>
−
<cmath>A'= I_\Omega (A), D'= I_\Omega (D), C = I_\omega (C) \implies</cmath>
+
<cmath>A'= I_\Omega (A), D'= I_\Omega (D), C = I_\Omega (C) \implies</cmath>
−
<cmath>AA' \cdot AB = BC^2,  \angle BDA = \angle BA'D'.</cmath>
+
<cmath>BA' \cdot AB = BC^2,  \angle BDA = \angle BA'D'.</cmath>
 
Let <math>\theta</math> be the circle <math>ABCD.</math>
 
Let <math>\theta</math> be the circle <math>ABCD.</math>
  
Line 49: Line 49:
 
<cmath>\angle BA'D' = \angle BA'C = \angle BDA.</cmath>
 
<cmath>\angle BA'D' = \angle BA'C = \angle BDA.</cmath>
 
<math>ABCD</math> is cyclic <math>\implies \angle BA'C = \angle AB'D.</math>
 
<math>ABCD</math> is cyclic <math>\implies \angle BA'C = \angle AB'D.</math>
−
<math>AB' + BA' = \frac {AD^2 + BC^2 }{AB} = AB \implies</math> points <math>A'</math> and <math>B'</math> are coincide.
+
<cmath>AB' + BA' = \frac {AD^2 + BC^2 }{AB} = AB \implies</cmath> points <math>A'</math> and <math>B'</math> are coincide.
  
 
Denote <math>A' = B' = Q \in AB.</math>
 
Denote <math>A' = B' = Q \in AB.</math>
  
−
Suppose, we move <math>P</math> from <math>A</math> to <math>B.</math> Then <math>\angle AQD</math> decreases monotonically, <math>\angle AQC</math> increases monotonically. So, there is only one point where <cmath>\angle AQD = \angle BQC \implies P = Q.</cmath>
+
Suppose, we move point <math>Q</math> from <math>A</math> to <math>B.</math> Then <math>\angle AQD</math> decreases monotonically, <math>\angle BQC</math> increases monotonically. So, there is only one point where <cmath>\angle AQD = \angle BQC \implies P = Q.</cmath>
  
 
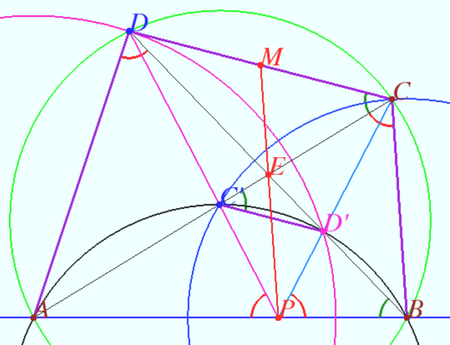
<cmath>B = I_\omega (P), D' = I_\omega (D'), C' = I_\omega (C), A = I_\omega (\infty) \implies</cmath>
 
<cmath>B = I_\omega (P), D' = I_\omega (D'), C' = I_\omega (C), A = I_\omega (\infty) \implies</cmath>
−
<math>\hspace{10mm} I_\omega (CD'P) = AC'D'B</math> is cyclic.
+
<math>\hspace{19mm} I_\omega (CD'P) = AC'D'B</math> is cyclic.
 
<cmath>\angle ACD = \angle ABD = \angle CC'D \implies C' D' || CD \implies</cmath>
 
<cmath>\angle ACD = \angle ABD = \angle CC'D \implies C' D' || CD \implies</cmath>
−
<math>\hspace{10mm} C'D'CD</math> is  trapezoid.
+
<math>\hspace{19mm} C'D'CD</math> is  trapezoid.
  
 
It is known that the intersection of the diagonals, intersection point of the lines containing the lateral sides of the trapezoid and the midpoints of two parallel sides are collinear.
 
It is known that the intersection of the diagonals, intersection point of the lines containing the lateral sides of the trapezoid and the midpoints of two parallel sides are collinear.
Line 66: Line 66:
 
==See also==
 
==See also==
 
{{USAMO newbox|year=2019|num-b=1|num-a=3}}
 
{{USAMO newbox|year=2019|num-b=1|num-a=3}}
 +
 +
{{MAA Notice}}

Latest revision as of 22:51, 18 October 2022

Problem

Let $ABCD$ be a cyclic quadrilateral satisfying $AD^2 + BC^2 = AB^2$. The diagonals of $ABCD$ intersect at $E$. Let $P$ be a point on side $\overline{AB}$ satisfying $\angle APD = \angle BPC$. Show that line $PE$ bisects $\overline{CD}$.

Solution

Let $PE \cap DC = M$. Also, let $N$ be the midpoint of $AB$. Note that only one point $P$ satisfies the given angle condition. With this in mind, construct $P'$ with the following properties:

(1) $AP' \cdot AB = AD^2$

(2) $BP' \cdot AB = CD^2$

Claim: $P = P'$

Proof: The conditions imply the similarities $ADP \sim ABD$ and $BCP \sim BAC$ whence $\measuredangle APD = \measuredangle BDA = \measuredangle BCA = \measuredangle CPB$ as desired. $\square$

Claim: $PE$ is a symmedian in $AEB$

Proof: We have \begin{align*} AP \cdot AB = AD^2 \iff AB^2 \cdot AP &= AD^2 \cdot AB \\ \iff \left( \frac{AB}{AD} \right)^2 &= \frac{AB}{AP} \\ \iff \left( \frac{AB}{AD} \right)^2 - 1 &= \frac{AB}{AP} - 1 \\ \iff \frac{AB^2 - AD^2}{AD^2} &= \frac{BP}{AP} \\ \iff \left(\frac{BC}{AD} \right)^2 &= \left(\frac{BE}{AE} \right)^2 = \frac{BP}{AP} \end{align*} as desired. $\square$

Since $P$ is the isogonal conjugate of $N$, $\measuredangle PEA = \measuredangle MEC = \measuredangle BEN$. However $\measuredangle MEC = \measuredangle BEN$ implies that $M$ is the midpoint of $CD$ from similar triangles, so we are done. $\square$

Solution 2

2019 USAMO 2.png
2019 USAMO 2a.png

Let $\omega$ be the circle centered at $A$ with radius $AD.$

Let $\Omega$ be the circle centered at $B$ with radius $BC.$

We denote $I_\omega$ and $I_\Omega$ inversion with respect to $\omega$ and $\Omega,$ respectively. \[B'= I_\omega (B), C'= I_\omega (C), D = I_\omega (D) \implies\] \[AB' \cdot AB = AD^2, \angle ACB = \angle AB'C'.\] \[A'= I_\Omega (A), D'= I_\Omega (D), C = I_\Omega (C) \implies\] \[BA' \cdot AB = BC^2, \angle BDA = \angle BA'D'.\] Let $\theta$ be the circle $ABCD.$

$I_\omega (\theta) = B'C'D,$ straight line, therefore \[\angle AB'C' = \angle AB'D' = \angle ACB.\] $I_\Omega (\theta) = A'D'C,$ straight line, therefore \[\angle BA'D' = \angle BA'C = \angle BDA.\] $ABCD$ is cyclic $\implies \angle BA'C = \angle AB'D.$ \[AB' + BA' = \frac {AD^2 + BC^2 }{AB} = AB \implies\] points $A'$ and $B'$ are coincide.

Denote $A' = B' = Q \in AB.$

Suppose, we move point $Q$ from $A$ to $B.$ Then $\angle AQD$ decreases monotonically, $\angle BQC$ increases monotonically. So, there is only one point where \[\angle AQD = \angle BQC \implies P = Q.\]

\[B = I_\omega (P), D' = I_\omega (D'), C' = I_\omega (C), A = I_\omega (\infty) \implies\] $\hspace{19mm} I_\omega (CD'P) = AC'D'B$ is cyclic. \[\angle ACD = \angle ABD = \angle CC'D \implies C' D' || CD \implies\] $\hspace{19mm} C'D'CD$ is trapezoid.

It is known that the intersection of the diagonals, intersection point of the lines containing the lateral sides of the trapezoid and the midpoints of two parallel sides are collinear.

vladimir.shelomovskii@gmail.com, vvsss

See also

2019 USAMO (Problems • Resources)
Preceded by
Problem 1 		Followed by
Problem 3
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2019_USAMO_Problems/Problem_2&oldid=179229"