2020 IMO Problems/Problem 1
Contents
Problem
Consider the convex quadrilateral ![]() . The point
. The point ![]() is in the interior of
is in the interior of ![]() . The following ratio equalities hold:
. The following ratio equalities hold:
![]() Prove that the following three lines meet in a point: the internal bisectors of angles
Prove that the following three lines meet in a point: the internal bisectors of angles ![]() and
and ![]() and the perpendicular bisector of segment
and the perpendicular bisector of segment ![]() .
.
solution 1
Let the perpendicular bisector of ![]() meet at point
meet at point ![]() , those two lined meet at
, those two lined meet at ![]() at
at ![]() respectively.
respectively.
As the problem states, denote that ![]() . We can express another triple with
. We can express another triple with ![]() as well. Since the perpendicular line of
as well. Since the perpendicular line of ![]() meets
meets ![]() at point
at point ![]() ,
, ![]() , which means that points
, which means that points ![]() are concyclic since
are concyclic since ![]()
Similarly, points ![]() are concyclic as well, which means five points
are concyclic as well, which means five points ![]() are concyclic.,
are concyclic., ![]()
Moreover, since ![]() ,
, ![]() so the angle bisector if the angle
so the angle bisector if the angle ![]() must be the perpendicular line of
must be the perpendicular line of ![]() , so as the angle bisector of
, so as the angle bisector of ![]() , which means those three lines must be concurrent at the circumcenter of the circle containing five points
, which means those three lines must be concurrent at the circumcenter of the circle containing five points ![]() as desired
as desired
~ bluesoul
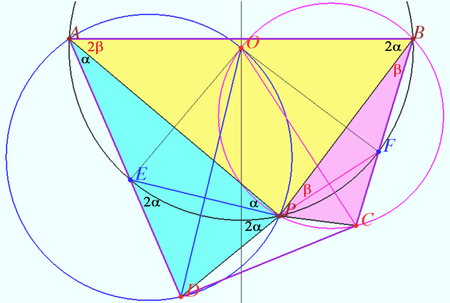
Solution 2 (Three perpendicular bisectors)
The essence of the proof is the replacement of the bisectors of angles by the perpendicular bisectors of the sides of the cyclic pentagon.
Let ![]() be the circumcenter of
be the circumcenter of ![]() is the perpendicular bisector of
is the perpendicular bisector of ![]() and point
and point ![]() lies on
lies on ![]() Then
Then
![]()
![]() is cyclic.
is cyclic.
![]() the bisector of the
the bisector of the ![]() is the perpendicular bisector of the side
is the perpendicular bisector of the side ![]() of the cyclic
of the cyclic ![]() that passes through the center
that passes through the center ![]()
A similar reasoning can be done for ![]() the perpendicular bisector of
the perpendicular bisector of ![]()
vladimir.shelomovskii@gmail.com, vvsss
Video solution
https://youtu.be/bDHtM1wijbY [Shorter solution, video covers all day 1 problems]
See Also
| 2020 IMO (Problems) • Resources | ||
| Preceded by First Problem |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 2 |
| All IMO Problems and Solutions | ||