2021 Fall AMC 12A Problems/Problem 13
Contents
Problem
The angle bisector of the acute angle formed at the origin by the graphs of the lines ![]() and
and ![]() has equation
has equation ![]() What is
What is ![]()
![]()
Diagram
![[asy] /* Made by MRENTHUSIASM */ size(250); real xMin = -1; real xMax = 4; real yMin = -1; real yMax = 4; real k = (1+sqrt(5))/2; pair O; O = origin; draw(anglemark(dir((1,1)),O,dir((1,k)),20), red); draw(anglemark(dir((1,k)),O,dir((1,3)),20), red); add(pathticks(anglemark(dir((1,1)),O,dir((1,k)),20), n = 1, r = 0.05, s = 5, red)); add(pathticks(anglemark(dir((1,k)),O,dir((1,3)),20), n = 1, r = 0.05, s = 5, red)); draw((xMin,0)--(xMax,0),black+linewidth(1.5),EndArrow(5)); draw((0,yMin)--(0,yMax),black+linewidth(1.5),EndArrow(5)); label("$x$",(xMax,0),(2,0)); label("$y$",(0,yMax),(0,2)); label("$y=x$",4*dir((1,1))); label("$y=3x$",4*dir((1,3))); label("$y=kx$",4*dir((1,k))); draw(O--3.75*dir((1,1))^^O--3.75*dir((1,3))^^O--3.75*dir((1,k))); [/asy]](http://latex.artofproblemsolving.com/e/d/8/ed8c030315c6a7a32e49ccbd13eeb76fd3d85b39.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1 (Angle Bisector Theorem)
This solution refers to the Diagram section.
Let ![]() and
and ![]() As shown below, note that
As shown below, note that ![]() and
and ![]() are on the lines
are on the lines ![]() and
and ![]() respectively. By the Distance Formula, we have
respectively. By the Distance Formula, we have ![]() and
and ![]()
![[asy] /* Made by MRENTHUSIASM */ size(250); real xMin = -1; real xMax = 4; real yMin = -1; real yMax = 4; real k = (1+sqrt(5))/2; pair O, A, B, C; O = origin; A = (3,3); B = (1,3); C = (3/k,3); draw(anglemark(dir((1,1)),O,dir((1,k)),20), red); draw(anglemark(dir((1,k)),O,dir((1,3)),20), red); dot("$O$",O,1.5*SW,linewidth(5)); dot("$A$",A,1.5*N,linewidth(5)); dot("$B$",B,1.5*N,linewidth(5)); dot("$C$",C,1.5*N,linewidth(5)); add(pathticks(anglemark(dir((1,1)),O,dir((1,k)),20), n = 1, r = 0.05, s = 5, red)); add(pathticks(anglemark(dir((1,k)),O,dir((1,3)),20), n = 1, r = 0.05, s = 5, red)); draw((xMin,0)--(xMax,0),black+linewidth(1.5),EndArrow(5)); draw((0,yMin)--(0,yMax),black+linewidth(1.5),EndArrow(5)); draw(A--B--O--cycle^^O--C); label("$x$",(xMax,0),(2,0)); label("$y$",(0,yMax),(0,2)); label("$3\sqrt{2}$",midpoint(O--A),1.5*E,red+fontsize(10)); label("$\sqrt{10}$",midpoint(O--B),W,red+fontsize(10)); label("$3-\frac3k$",midpoint(A--C),N,red+fontsize(10)); label("$\frac3k-1$",midpoint(B--C),N,red+fontsize(10)); [/asy]](http://latex.artofproblemsolving.com/a/a/c/aac41ac1e6c93666dc86d3bf7c0c26062f339664.png) By the Angle Bisector Theorem, we get
By the Angle Bisector Theorem, we get ![]() or
or
 Since
Since ![]() the answer is
the answer is 
Remark
The value of ![]() is known as the Golden Ratio:
is known as the Golden Ratio: ![]()
~MRENTHUSIASM
Solution 2 (Analytic and Plane Geometry)
![[asy] size(180); real xMin = -0.5; real xMax = 2; real yMin = -0.5; real yMax = 4.5; real k = (1+sqrt(5))/2; real m = sqrt(2); real n = sqrt(10); real q = sqrt((5+sqrt(5))/2); pair O; O = origin; draw((xMin,0)--(xMax,0),black+linewidth(1.5),EndArrow(5)); draw((0,yMin)--(0,yMax),black+linewidth(1.5),EndArrow(5)); label("$O$",(-0.2,-0.2),(0,0)); label("$x$",(xMax,0),(2,0)); label("$y$",(0,yMax),(0,2)); label("$A$",(1,0.95),(1,1)); label("$B$",(1,2.80),(1,3)); label("$C$",(1.06,k-0.05),(1,k)); draw(O--m*dir((1,1))^^O--n*dir((1,3))^^O--q*dir((1,k))); draw((1,1)--(1,3)); [/asy]](http://latex.artofproblemsolving.com/a/7/0/a704fe951a038435a7c1011a84366eecaea2521c.png) Consider the graphs of
Consider the graphs of ![]() and
and ![]() . Since it will be easier to consider at unity, let
. Since it will be easier to consider at unity, let ![]() , then we have
, then we have ![]() and
and ![]() .
.
Now, let ![]() be
be ![]() ,
, ![]() be
be ![]() , and
, and ![]() be
be ![]() . Cutting through side
. Cutting through side ![]() of triangle
of triangle ![]() is the angle bisector
is the angle bisector ![]() where
where ![]() is on side
is on side ![]() .
.
Hence, by the Angle Bisector Theorem, we get ![]() .
.
By the Pythagorean Theorem, ![]() and
and ![]() . Therefore,
. Therefore, ![]() .
.
Since ![]() , it is easy derive
, it is easy derive ![]() .
.
The vertical distance between the ![]() -axis and
-axis and ![]() is
is ![]() . Because the
. Because the ![]() -coordinate of point
-coordinate of point ![]() is
is ![]() , the slope we need to find is just the
, the slope we need to find is just the ![]() -coordinate
-coordinate 
~Wilhelm Z
Solution 3 (Analytic and Plane Geometry)
Let's begin by drawing a triangle that starts at the origin. Assume that the base of the triangle goes to the point ![]() . The line
. The line ![]() is the hypotenuse of a right triangle with side length
is the hypotenuse of a right triangle with side length ![]() . The hypotenuse' length is
. The hypotenuse' length is ![]() . Then, let's draw the line
. Then, let's draw the line ![]() . We extend it to when
. We extend it to when ![]() . The length of the hypotenuse of the larger triangle is
. The length of the hypotenuse of the larger triangle is ![]() with legs
with legs ![]() . We then draw the angle bisector. We should label the triangle, so here we go.
. We then draw the angle bisector. We should label the triangle, so here we go. ![]() is
is ![]() .
. ![]() is
is ![]() .
. ![]() is
is ![]() . When the line with angle
. When the line with angle ![]() intersects the line
intersects the line ![]() , call the point
, call the point ![]() . When the angle bisector intersects the line
. When the angle bisector intersects the line ![]() , call the point
, call the point ![]() . By Angle Bisector Theorem,
. By Angle Bisector Theorem, ![]() . Since
. Since ![]() is
is ![]() and
and ![]() is
is ![]() , we have that
, we have that ![]() is
is ![]() . Solving for
. Solving for ![]() , we get that
, we get that ![]() is
is ![]() .
.
Since ![]() is
is ![]() , we have that
, we have that ![]() is just one more than that. Therefore,
is just one more than that. Therefore, ![]() is
is ![]() . Since
. Since ![]() is
is ![]() , we get that
, we get that ![]() is
is  .
.
Remark: The answer turns out to be the golden ratio or phi (![]() ). Phi has many properties and is related to the Fibonacci sequence. See Phi.
). Phi has many properties and is related to the Fibonacci sequence. See Phi.
~Arcticturn ![]()
Solution 4 (Distance Between a Point and a Line)
Note that the distance between the point ![]() to line
to line ![]() is
is ![]() Because line
Because line ![]() is a perpendicular bisector, a point on the line
is a perpendicular bisector, a point on the line ![]() must be equidistant from the two lines(
must be equidistant from the two lines(![]() and
and ![]() ), call this point
), call this point ![]() Because, the line
Because, the line ![]() passes through the origin, our requested value of
passes through the origin, our requested value of ![]() which is the slope of the angle bisector line, can be found when evaluating the value of
which is the slope of the angle bisector line, can be found when evaluating the value of ![]() By the Distance from Point to Line formula we get the equation,
By the Distance from Point to Line formula we get the equation, ![]() Note that
Note that ![]() because
because ![]() is higher than
is higher than ![]() and
and ![]() because
because ![]() is lower to
is lower to ![]() Thus, we solve the equation,
Thus, we solve the equation, ![]() Thus, the value of
Thus, the value of ![]() Thus, the answer is
Thus, the answer is 
(Fun Fact: The value ![]() is the golden ratio
is the golden ratio ![]() )
)
~NH14
Solution 5 (Trigonometry)
Denote by ![]() ,
, ![]() ,
, ![]() the acute angles formed between the
the acute angles formed between the ![]() -axis and lines
-axis and lines ![]() ,
, ![]() ,
, ![]() , respectively.
Hence,
, respectively.
Hence, ![]() ,
, ![]() ,
, ![]() .
.
Denote by ![]() the acute angle formed by lines
the acute angle formed by lines ![]() and
and ![]() .
.
Hence,

Following from the double-angle identity, we have
![]()
Hence, ![]() .
.
Because ![]() is acute,
is acute, ![]() is acute.
Hence,
is acute.
Hence, ![]() .
Hence,
.
Hence, ![]() .
.
Because line ![]() is the angle bisector of
is the angle bisector of ![]() , the angle between lines
, the angle between lines ![]() and
and ![]() is
is ![]() .
.
Hence,

Therefore, the answer is  .
.
~Steven Chen (www.professorchenedu.com)
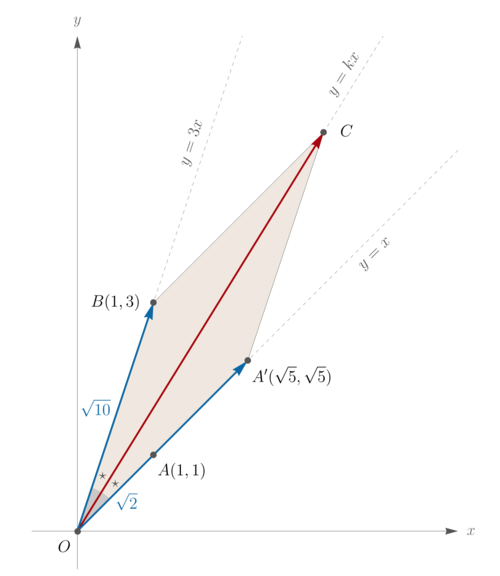
Solution 6 (Vectors)
When drawing the lines ![]() and
and ![]() , it is natural to choose points
, it is natural to choose points ![]() and
and ![]() together with origin
together with origin ![]() . See the figure attached.
We utilize the fact that if
. See the figure attached.
We utilize the fact that if ![]() and
and ![]() are vectors of same length, then
are vectors of same length, then ![]() bisects the angle between
bisects the angle between ![]() and
and ![]() .
.
In particular, we scale the vector ![]() by the factor of
by the factor of ![]() to get
to get ![]() .
So by adding vectors
.
So by adding vectors ![]() and
and ![]() we get
we get
![]() which bisects the acute angle formed by lines
which bisects the acute angle formed by lines ![]() and
and ![]() . (In other words, quadrilateral
. (In other words, quadrilateral ![]() is a rhombus.)
Finally, observe that
is a rhombus.)
Finally, observe that ![]() lies on the line
lies on the line ![]() whose slope is
whose slope is
![]() Thus, the answer is
Thus, the answer is  .
. ![]()
~VensL.
See Also
| 2021 Fall AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 12 |
Followed by Problem 14 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.