2021 IMO Problems/Problem 3
Problem
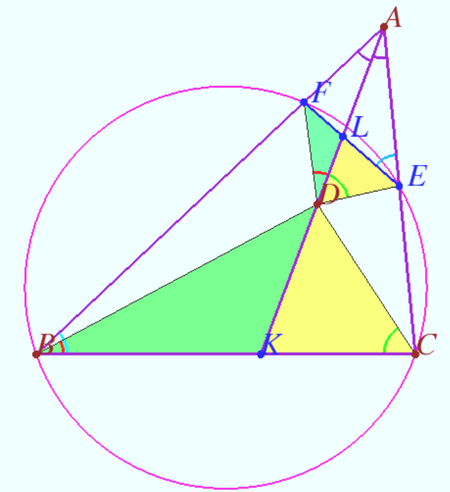
Let ![]() be an interior point of the acute triangle
be an interior point of the acute triangle ![]() with
with ![]() so that
so that ![]() . The point
. The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() , the point
, the point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() , and the point
, and the point ![]() on the line
on the line ![]() satisfies
satisfies ![]() . Let
. Let ![]() and
and ![]() be the circumcentres of the triangles
be the circumcentres of the triangles ![]() and
and ![]() respectively. Prove that the lines
respectively. Prove that the lines ![]() ,
, ![]() , and
, and ![]() are concurrent.
are concurrent.
Solution
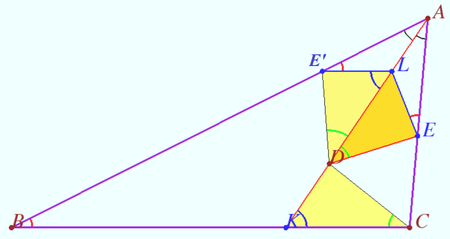
Lemma
Let ![]() be bisector of the triangle
be bisector of the triangle ![]() , point
, point ![]() lies on
lies on ![]() The point
The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() . The point
. The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() The point
The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() Then
Then ![]() and
and ![]() are antiparallel with respect to the sides of an angle
are antiparallel with respect to the sides of an angle ![]() and
and ![]() Proof
Proof
Symmetry of points ![]() and
and ![]() with respect bisector
with respect bisector ![]() implies
implies ![]()
![]()
![]()
![]()
![]() Corollary
Corollary
In the given problem ![]() and
and ![]() are antiparallel with respect to the sides of an angle
are antiparallel with respect to the sides of an angle ![]() quadrangle
quadrangle ![]() is concyclic.
is concyclic.
Shelomovskii, vvsss, www.deoma-cmd.ru
Video solution
https://youtu.be/cI9p-Z4-Sc8 [Video contains solutions to all day 1 problems]