2021 JMPSC Sprint Problems
- This is a twenty question free-response test. Each question has exactly one integer answer.
- You have 50 minutes to complete the test.
- You will receive 3 points for each correct answer, and 0 points for each problem left unanswered or incorrect.
- Figures are not necessarily drawn to scale.
- No aids are permitted other than scratch paper, graph paper, rulers, and erasers. No calculators, smartwatches, or computing devices are allowed. No problems on the test will require the use of a calculator.
Contents
Problem 1
Compute ![]() .
.
Problem 2
Brady has an unlimited supply of quarters ($0.25), dimes ($0.10), nickels ($0.05), and pennies ($0.01). What is the least number (quantity, not type) of coins Brady can use to pay off $![]() ?
?
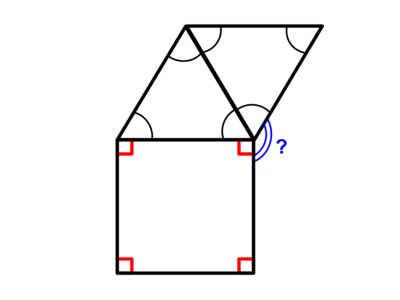
Problem 3
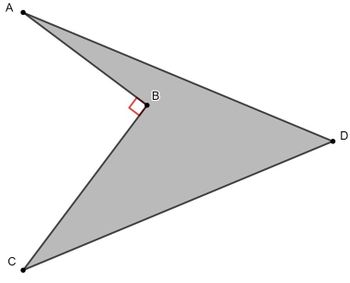
If all angles marked with a red square are ![]() and all angles marked with one black curve are equal, find the measure of the angle with a question mark.
and all angles marked with one black curve are equal, find the measure of the angle with a question mark.
Problem 4
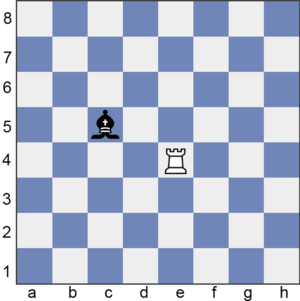
A standard chess-board is an 8 by 8 grid of squares. A bishop is placed at square C5 (row 5, column C) and a rook is placed at square E4 (row 4, column E). How many squares can be attacked by both the bishop and rook if they each take one move?
(The bishop can attack any square in the same diagonal as itself, including squares A7, F8, G1, D6, and so on. The rook can attack any square in the same row or column as itself, including squares E5, E8, E4, C4, and so on.)
Problem 5
What two-digit even number has digits that sum to ![]() ?
?
Problem 6
Luis has ![]() coins that are all either nickels or dimes. If the probability of randomly picking a nickel from these
coins that are all either nickels or dimes. If the probability of randomly picking a nickel from these ![]() coins is
coins is ![]() how much money does Luis have in dollars?
how much money does Luis have in dollars?
Problem 7
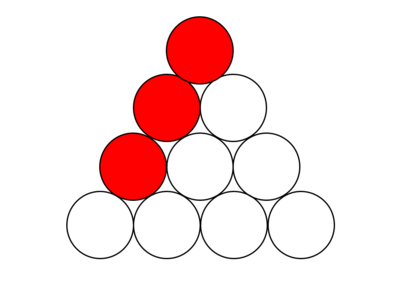
How many sets of three circles are in the diagram below such that their centers lie on the same line and each circle in the set is adjacent to another circle in the set? (Assume that if the centers of three circles appear to be on the same line, then they are on the same line. For example, the three red shaded circles count as one such set.)
Problem 8
How many positive two-digit numbers exist such that the product of its digits is not zero?
Problem 9
A machine cuts a piece of metal at a constant rate. After leaving the machine alone for twenty minutes, the metal has been split into six pieces. How many more minutes will it take until there are twenty pieces?
Problem 10
Serena gets a grade of ![]() for her chapter test. She doesn't remember how many problems there were, but she remembers that there were at most
for her chapter test. She doesn't remember how many problems there were, but she remembers that there were at most ![]() problems, each problem solved correctly was worth an equal amount of points, and she did not receive any points for an incorrect or skipped question. Find the sum of all the possible numbers of problems that the test could have had.
problems, each problem solved correctly was worth an equal amount of points, and she did not receive any points for an incorrect or skipped question. Find the sum of all the possible numbers of problems that the test could have had.
Problem 11
How many numbers are in the finite sequence of consecutive perfect squares ![]()
Problem 12
The solution to the equation ![]() can be written as
can be written as ![]() , where
, where ![]() is a real number. What is
is a real number. What is ![]() ?
?
Problem 13
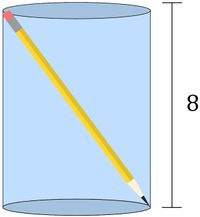
Grace places a pencil in a cylindrical cup and is surprised to see that it fits diagonally. The pencil is ![]() units long and of negligible thickness. The cup is
units long and of negligible thickness. The cup is ![]() units tall. The volume of the cup can be written as
units tall. The volume of the cup can be written as ![]() cubic units. Find
cubic units. Find ![]() .
.
Problem 14
Ari, Bryant, Chandler, and David each tell one truth and one lie.
- Ari: Bryant is the tallest among the four of us. Chandler is the shortest among the four of us.
- Bryant: Ari is the oldest in the room. Ari is the shortest in the room.
- Chandler: David is taller than me. David is older than me.
- David: Chandler told two truths. I am the oldest person in the room.
If the first name of the shortest person is ![]() letters long and the first name of the second-tallest person is
letters long and the first name of the second-tallest person is ![]() letters long, find
letters long, find ![]() (Assume that no two people share the same height and are born on the same day.)
(Assume that no two people share the same height and are born on the same day.)
Problem 15
Find the last two digits of ![]()
Problem 16
![]() is a concave quadrilateral with
is a concave quadrilateral with ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Find the area of
. Find the area of ![]() .
.
Problem 17
What is the smallest positive multiple of ![]() that has no zeros in its decimal representation?
that has no zeros in its decimal representation?
Problem 18
On square ![]() with side length
with side length ![]() ,
, ![]() is the midpoint of
is the midpoint of ![]() . Let
. Let ![]() be the foot of the altitude from
be the foot of the altitude from ![]() to
to ![]() . If
. If ![]() can be represented as
can be represented as ![]() for some integer
for some integer ![]() find the value of
find the value of ![]()
Problem 19
As an April Fool’s prank, Sean hacks his teacher’s digital clock and switches each digit to a certain letter. Right now, the hacked clock displays ![]() .
. ![]() minutes later, it displays
minutes later, it displays ![]() . If no two digits represent the same letter, find the value of
. If no two digits represent the same letter, find the value of ![]()
Problem 20
For all integers ![]() and
and ![]() , define the operation
, define the operation ![]() as
as ![]() Find
Find ![]()
See also
- 2021 JMPSC Accuracy Problems
- 2021 JMPSC Invitationals Problems
- 2021 JMPSC Sprint Answer Key
- All JMPSC Problems and Solutions
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition.