2021 USAMO Problems/Problem 1
Revision as of 13:32, 25 December 2023 by Integralarefun (talk | contribs) (→Solution: SEVERE LaTeX formatting fixing)
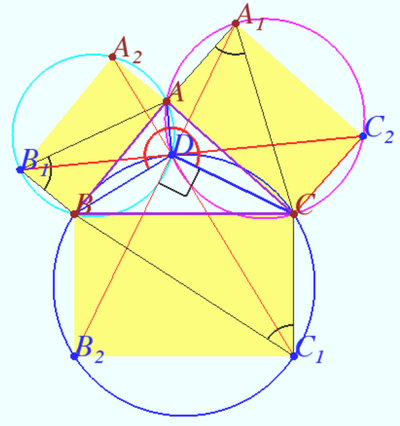
Rectangles ![]()
![]() and
and ![]() are erected outside an acute triangle
are erected outside an acute triangle ![]() Suppose that
Suppose that![]() Prove that lines
Prove that lines ![]()
![]() and
and ![]() are concurrent.
are concurrent.
Solution
Let ![]() be the second point of intersection of the circles
be the second point of intersection of the circles ![]() and
and ![]() Then:
Then:
 Therefore,
Therefore, ![]() is cyclic with diameters
is cyclic with diameters ![]() and
and ![]() , and thus
, and thus ![]() Similarly,
Similarly, ![]() , meaning points
, meaning points ![]() ,
, ![]() , and
, and ![]() are collinear.
are collinear.
Similarly, the points ![]() and
and ![]() are collinear.
are collinear.
(After USAMO 2021 Solution Notes – Evan Chen)
vladimir.shelomovskii@gmail.com, vvsss
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.