Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Isogonal conjugate

Revision as of 17:31, 7 February 2023 by Vvsss (talk | contribs) (→‎Distance to the sides of the triangle)

Isogonal conjugates are pairs of points in the plane with respect to a certain triangle.

Definition of isogonal conjugate of a point

Definitin 1.png

Let $P$ be a point in the plane, and let $ABC$ be a triangle. We will denote by $a,b,c$ the lines $BC, CA, AB$. Let $p_a, p_b, p_c$ denote the lines $PA$, $PB$, $PC$, respectively. Let $q_a$, $q_b$, $q_c$ be the reflections of $p_a$, $p_b$, $p_c$ over the angle bisectors of angles $A$, $B$, $C$, respectively. Then lines $q_a$, $q_b$, $q_c$ concur at a point $Q$, called the isogonal conjugate of $P$ with respect to triangle $ABC$.

Proof

By our constructions of the lines $q$, $\angle p_a b \equiv \angle q_a c$, and this statement remains true after permuting $a,b,c$. Therefore by the trigonometric form of Ceva's Theorem \[\frac{\sin \angle q_a b}{\sin \angle c q_a} \cdot \frac{\sin \angle q_b c}{\sin \angle a q_b} \cdot \frac{\sin \angle q_c a}{\sin \angle b q_c} = \frac{\sin \angle p_a c}{\sin \angle b p_a} \cdot \frac{\sin \angle p_b a}{\sin \angle c p_b} \cdot \frac{\sin \angle p_c b}{\sin \angle a p_c} = 1,\] so again by the trigonometric form of Ceva, the lines $q_a, q_b, q_c$ concur, as was to be proven. $\blacksquare$

Second definition

Definition 2.png

Let triangle $\triangle ABC$ be given. Let point $P$ lies in the plane of $\triangle ABC,$ \[P \notin AB, P \notin BC, P \notin AC.\] Let the reflections of $P$ in the sidelines $BC, CA, AB$ be $P_1, P_2, P_3.$

Then the circumcenter $Q$ of the $\triangle P_1P_2P_3$ is the isogonal conjugate of $P.$

Points $A, B,$ and $C$ have not isogonal conjugate points.

Another points of sidelines $BC, AC, AB$ have points $A, B, C,$ respectively as isogonal conjugate points.

Proof \[PC = P_1C, PC = P_2C \implies P_1C = P_2C.\] \[\angle ACQ = \angle BCP_1 \implies \angle QCP_1 = \angle ACB.\] \[\angle BCQ = \angle ACP_2 \implies \angle QCP_2 = \angle ACB.\] $\angle QCP_1 = \angle QCP_2, CP_1 = CP_2, QC$ common $\implies$ \[\triangle QCP_1 = \triangle QCP_2 \implies QP_1 = QP_2.\] Similarly $QP_1 = QP_3 \implies Q$ is the circumcenter of the $\triangle P_1P_2P_3.$ $\blacksquare$

Let point $P$ be the point with barycentric coordinates $(p : q : r),$ \[p = [(P-B),(P-C)], q = [(P-C),(P-A)], r = [(P-A),(P-B)].\] Then $Q$ has barycentric coordinates \[(p' : q' : r'), p' = \frac {|B - C|^2}{p}, q' = \frac {|A-C|^2}{q}, r' = \frac {|A - B|^2}{r}.\]

vladimir.shelomovskii@gmail.com, vvsss

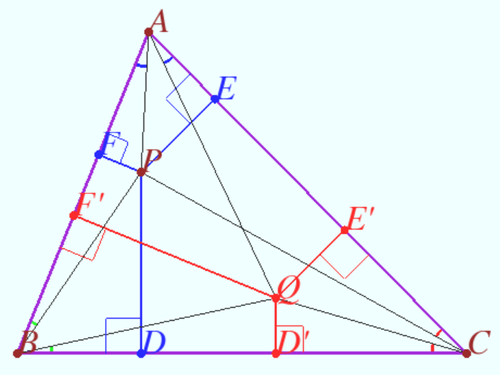
Distance to the sides of the triangle

Distances to.png

Let $Q$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$

Let $E$ and $D$ be the projection $P$ on sides $AC$ and $BC,$ respectively.

Let $E'$ and $D'$ be the projection $Q$ on sides $AC$ and $BC,$ respectively.

Then $\frac {PE}{PD} = \frac{QD'}{QE'}.$

Proof

Let $\theta = \angle ACP = \angle BCQ, \Theta = \angle ACQ = \angle BCP.$ \[\frac {PE}{PD} = \frac {PC \sin \theta}{PC \sin \Theta} = \frac {QC \sin \theta}{QC \sin \Theta} = \frac {QD'}{QE'}.\] vladimir.shelomovskii@gmail.com, vvsss

Sign of isogonally conjugate points

Isog dist.png

Let triangle $\triangle ABC$ and points $P$ and $Q$ inside it be given.

Let $D, E, F$ be the projections $P$ on sides $BC, AC, AB,$ respectively. Let $D', E', F'$ be the projections $Q$ on sides $BC, AC, AB,$ respectively.

Let $\frac {PE}{PD} = \frac{QD'}{QE'}, \frac {PF}{PD} = \frac{QD'}{QF'}.$

Prove that point $Q$ is the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$ One can prove similar theorem in the case $P$ outside $\triangle ABC.$

Proof

Circumcircle of pedal triangles

Common circle.png

Let $Q$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$ Let $E, D, F$ be the projection $P$ on sides $AC, BC, AB,$ respectively.

Let $E', D', F'$ be the projection $Q$ on sides $AC, BC, AB,$ respectively.

Then points $D, D', E, E', F, F'$ are concyclic.

The midpoint $PQ$ is circumcenter of $DD'EE'FF'.$

Proof

Let $\theta = \angle ACP = \angle BCQ, \Theta = \angle ACQ = \angle BCP.$ $CE \cdot CE' = PC \cos \theta \cdot QC \cos \Theta = PC \cos \Theta \cdot QC \cos \theta = CD \cdot CD'.$ Hence points $D, D', E, E'$ are concyclic.

$PQE'E$ is trapezoid, $E'E \perp PE \implies OE = OE' \implies$

the midpoint $PQ$ is circumcenter of $DD'EE'.$

Similarly points $D, D', F, F'$ are concyclic and points $F, F', E, E'$ are concyclic.

Therefore points $D, D', E, E', F, F'$ are concyclic, so the midpoint $PQ$ is circumcenter of $DD'EE'FF'.$

vladimir.shelomovskii@gmail.com, vvsss

Circles

2 points isogon.png

Let $Q$ be the isogonal conjugate of a point $P$ with respect to a triangle $\triangle ABC.$ Let $D$ be the circumcenter of $\triangle BCP.$ Let $E$ be the circumcenter of $\triangle BCQ.$ Prove that points $D$ and $E$ are inverses with respect to the circumcircle of $\triangle ABC.$

Proof

The circumcenter of $\triangle ABC$ point $O,$ and points $D$ and $E$ lies on the perpendicular bisector of $BC.$ \[\angle BOD = \angle COE = \angle BAC.\] \[2 \angle BDO = \angle BDC = \overset{\Large\frown} {BC} = 360^\circ - \overset{\Large\frown} {CB} = 360^\circ - 2 \angle BPC.\] \[\angle BDO = 180^\circ - \angle BPC = \angle PBC + \angle PCB.\] Similarly $\angle CEO = 180^\circ - \angle BQC = \angle QBC + \angle QCB.$ \[\angle PBC + \angle QBC = \angle PBC + \angle PBA = \angle ABC.\] \[\angle QCB + \angle PCB = \angle QCB + \angle QCA = \angle ACB.\]

\[\angle CEO +\angle BDO = \angle ABC + \angle ACB = 180^\circ - \angle BAC \implies\] \[\angle OBD = 180^\circ - \angle BOD - \angle BDO = \angle OEC \implies\] \[\triangle OBD \sim \triangle OEC \implies \frac {OB}{OE} = \frac {OD}{OC} \implies OD \cdot OE = OB^2. \blacksquare\]

vladimir.shelomovskii@gmail.com, vvsss

Problems

Olympiad

Given a nonisosceles, nonright triangle $ABC,$ let $O$ denote the center of its circumscribed circle, and let $A_1, \, B_1,$ and $C_1$ be the midpoints of sides $BC, \, CA,$ and $AB,$ respectively. Point $A_2$ is located on the ray $OA_1$ so that $\triangle OAA_1$ is similar to $\triangle OA_2A$. Points $B_2$ and $C_2$ on rays $OB_1$ and $OC_1,$ respectively, are defined similarly. Prove that lines $AA_2, \, BB_2,$ and $CC_2$ are concurrent, i.e. these three lines intersect at a point. (Source)

Let $P$ be a given point inside quadrilateral $ABCD$. Points $Q_1$ and $Q_2$ are located within $ABCD$ such that $\angle Q_1 BC = \angle ABP$, $\angle Q_1 CB = \angle DCP$, $\angle Q_2 AD = \angle BAP$, $\angle Q_2 DA = \angle CDP$. Prove that $\overline{Q_1 Q_2} \parallel \overline{AB}$ if and only if $\overline{Q_1 Q_2} \parallel \overline{CD}$. (Source)

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Isogonal_conjugate&oldid=188802"