Pascal's Triangle and Pythagorean Theorem
Contents
Pascal's Identity
Identity
Pascal's Identity states that

for any positive integers ![]() and
and ![]() . Here,
. Here, ![]() is the binomial coefficient
is the binomial coefficient  .
.
Remember that 
Proving it
If ![]() then
then  and so the result is pretty clear.
So assume
and so the result is pretty clear.
So assume ![]() . Then
. Then
 There we go. We proved it!
There we go. We proved it!
Why is it needed?
It's mostly just a cool thing to know. However, if you want to know how to use it in real life go to https://artofproblemsolving.com/videos/counting/chapter12/141. Or really any of the counting and probability videos.
Introduction to Pascal's Triangle
How to build it
Pascal's Triangle is a triangular array of numbers in which you start with two infinite diagonals of ones and each of the rest of the numbers is the sum of the two numbers above it. It looks something like this:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
And on and on...
Combinations
Combinations
Pascal's Triangle is really combinations. It looks something like this if it is depicted as combinations:
And on and on...
Proof
If you look at the way we build the triangle, each number is the sum of the two numbers above it. Assuming that these combinations are true then each combination in the sum of the two combinations above it. In an equation, it would look something like this:  . It's Pascals Identity! Therefore each row looks something like this:
. It's Pascals Identity! Therefore each row looks something like this:

Patterns and Properties
In addition to combinations, Pascal's Triangle has many more patterns and properties. See below. Be ready to be amazed.
Binomial Theorem
Let's multiply out some binomials. Try it yourself and it will not be fun:
![]()
![]()
![]()
![]()
If you take away the x's and y's you get:
1
1 1
1 2 1
1 3 3 1
It's Pascal's Triangle!
Proof
There are a number of different ways to prove the Binomial Theorem, for example by a straightforward application of mathematical induction. The Binomial Theorem also has a nice combinatorial proof:
We can write ![]() . Repeatedly using the distributive property, we see that for a term
. Repeatedly using the distributive property, we see that for a term ![]() , we must choose
, we must choose ![]() of the
of the ![]() terms to contribute an
terms to contribute an ![]() to the term, and then each of the other
to the term, and then each of the other ![]() terms of the product must contribute a
terms of the product must contribute a ![]() . Thus, the coefficient of
. Thus, the coefficient of ![]() is the number of ways to choose
is the number of ways to choose ![]() objects from a set of size
objects from a set of size ![]() , or
, or ![]() . Extending this to all possible values of
. Extending this to all possible values of ![]() from
from ![]() to
to ![]() , we see that
, we see that  , as claimed.
, as claimed.
Similarly, the coefficients of ![]() will be the entries of the
will be the entries of the ![]() row of Pascal's Triangle. This is explained further in the Counting and Probability textbook [AoPS]
row of Pascal's Triangle. This is explained further in the Counting and Probability textbook [AoPS]
In real life
It is really only used for multipling out binomials. More usage at https://artofproblemsolving.com/videos/counting/chapter14/126.
Powers of 2
Theorem
Theorem
It states that 
Why do we need it?
It is useful in many word problems (That means, yes, you can use it in real life) and it is just a cool thing to know. More at https://artofproblemsolving.com/videos/mathcounts/mc2010/419.
Proof
Subset proof
Say you have a word with n letters. How many subsets does it have in terms of n? Here is how you answer it: You ask the first letter Are you in or are you out? Same to the second letter. Same to the third. Same to the n. Each of the letters has two choices: In and Out. The would be ![]() ...n times.
...n times. ![]() .
.
Alternate proof
If you look at the way we built the triangle you see that each number is row n-1 is added on twice in row n. This means that each row doubles. That means you get powers of two.
Triangle Numbers
Theorem
If you look at the numbers in the third diagonal you see that they are triangle numbers.
Proof
Now we can make an equation: 
Hockey stick
For  .
.
![[asy] int chew(int n,int r){ int res=1; for(int i=0;i<r;++i){ res=quotient(res*(n-i),i+1); } return res; } for(int n=0;n<9;++n){ for(int i=0;i<=n;++i){ if((i==2 && n<8)||(i==3 && n==8)){ if(n==8){label(string(chew(n,i)),(11+n/2-i,-n),p=red+2.5);} else{label(string(chew(n,i)),(11+n/2-i,-n),p=blue+2);} } else{ label(string(chew(n,i)),(11+n/2-i,-n)); } } } [/asy]](http://latex.artofproblemsolving.com/d/d/6/dd6b10831339602460ad1a042dbf52340b246769.png)
This identity is known as the hockey-stick identity because, on Pascal's triangle, when the addends represented in the summation and the sum itself is highlighted, a hockey-stick shape is revealed.
Proof
Inductive Proof
This identity can be proven by induction on ![]() .
.
Base Case
Let ![]() .
.
 .
.
Inductive Step
Suppose, for some ![]() ,
,  .
Then
.
Then  .
.
Algebraic Proof
It can also be proven algebraically with Pascal's Identity,  .
Note that
.
Note that


 , which is equivalent to the desired result.
, which is equivalent to the desired result.
Combinatorial Proof 1
Imagine that we are distributing ![]() indistinguishable candies to
indistinguishable candies to ![]() distinguishable children. By a direct application of Balls and Urns, there are
distinguishable children. By a direct application of Balls and Urns, there are  ways to do this. Alternatively, we can first give
ways to do this. Alternatively, we can first give ![]() candies to the oldest child so that we are essentially giving
candies to the oldest child so that we are essentially giving ![]() candies to
candies to ![]() kids and again, with Balls and Urns,
kids and again, with Balls and Urns,  , which simplifies to the desired result.
, which simplifies to the desired result.
Combinatorial Proof 2
We can form a committee of size ![]() from a group of
from a group of ![]() people in
people in  ways. Now we hand out the numbers
ways. Now we hand out the numbers ![]() to
to ![]() of the
of the ![]() people. We can divide this into
people. We can divide this into ![]() disjoint cases. In general, in case
disjoint cases. In general, in case ![]() ,
, ![]() , person
, person ![]() is on the committee and persons
is on the committee and persons ![]() are not on the committee. This can be done in
are not on the committee. This can be done in  ways. Now we can sum the values of these
ways. Now we can sum the values of these ![]() disjoint cases, getting
disjoint cases, getting ![\[{{n+1}\choose {k+1}} ={{n}\choose{k}}+{{n-1}\choose{k}}+{{n-2}\choose{k}}+\hdots+{{k+1}\choose{k}}+{{k}\choose{k}}.\]](http://latex.artofproblemsolving.com/9/b/7/9b7df22b88e73aaeee483ca805a03c9601d0a02d.png)
See Also
AoPS Wiki
Videos
- https://artofproblemsolving.com/videos/counting/chapter12/141
- https://artofproblemsolving.com/videos/mathcounts/mc2012/374
- https://artofproblemsolving.com/videos/counting/chapter14/123
- https://artofproblemsolving.com/videos/counting/chapter13/143
- https://artofproblemsolving.com/videos/mathcounts/mc2010/419
Copied From
- 50 percent original made by Colball otherwise known as Colin Friesen
- Pascal's Identity
- Hockey-Stick Identity
- Pascal's Triangle
These are all on AoPS wiki. Look them up.
Now to Pythagorean Theorem.
What is the Pythagorean Theorem?
What is the Pythagorean Theorem?
The Pythagoras Theorem is also referred to as the Pythagorean Theorem![]() Pythagorean Theorem is used to find a side of any right triangle. It is
Pythagorean Theorem is used to find a side of any right triangle. It is ![]() , where
, where ![]() and
and ![]() are the legs of the triangle, and
are the legs of the triangle, and ![]() is the hypotenuse.
is the hypotenuse.
Why is it useful?
To find sides and angles of right triangles. Also, Trigonometry is pointless without it. If you know three angles of a triangle you can use the Pythagorean Theorem to find the sides or the area even if the angles are not right. It is probably the most famous Theorem in all of math!
Can we prove it?
Yes! The are hundreds of proves. I will just show you a few of them. Mathematicians even make a hobby of finding these proves. Even a US president made a published proof! Of, course this was a president in the 1800s because, well, presidents now are not really up to proving something like that. (You know, Trump and the others).
Proofs
Proof 1
We use ![]() to denote the area of triangle
to denote the area of triangle ![]() .
.
Let ![]() be the perpendicular to side
be the perpendicular to side ![]() from
from ![]() .
.
![[asy] pair A, B, C, H; A = (0, 0); B = (4, 3); C = (4, 0); H = foot(C, A, B); draw(A--B--C--cycle); draw(C--H); draw(rightanglemark(A, C, B)); draw(rightanglemark(C, H, B)); label("$A$", A, SSW); label("$B$", B, ENE); label("$C$", C, SE); label("$H$", H, NNW); [/asy]](http://latex.artofproblemsolving.com/a/1/9/a19bed9f5ac971139756a395da4e29366d45fc52.png)
Since ![]() are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths,
are similar right triangles, and the areas of similar triangles are proportional to the squares of corresponding side lengths,
![]() .
.
But since triangle ![]() is composed of triangles
is composed of triangles ![]() and
and ![]() ,
, ![]() , so
, so ![]() . ∎
. ∎
Proof 2
Consider a circle ![]() with center
with center ![]() and radius
and radius ![]() . Since
. Since ![]() and
and ![]() are perpendicular,
are perpendicular, ![]() is tangent to
is tangent to ![]() . Let the line
. Let the line ![]() meet
meet ![]() at
at ![]() and
and ![]() , as shown in the diagram:
, as shown in the diagram:
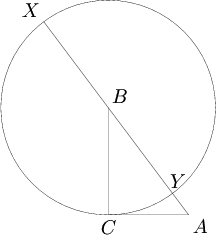
Evidently, ![]() and
and ![]() . By considering the power of point
. By considering the power of point ![]() with respect to
with respect to ![]() , we see
, we see
![]() . ∎
. ∎
Proof 3
![]() and
and ![]() are squares.
are squares.
![[asy] pair A, B,C,D; A = (-10,10); B = (10,10); C = (10,-10); D = (-10,-10); pair E,F,G,H; E = (7,10); F = (10, -7); G = (-7, -10); H = (-10, 7); draw(A--B--C--D--cycle); label("$A$", A, NNW); label("$B$", B, ENE); label("$C$", C, ESE); label("$D$", D, SSW); draw(E--F--G--H--cycle); label("$E$", E, N); label("$F$", F,SE); label("$G$", G, S); label("$H$", H, W); label("a", A--B,N); label("a", B--F,SE); label("a", C--G,S); label("a", H--D,W); label("b", E--B,N); label("b", F--C,SE); label("b", G--D,S); label("b", A--H,W); label("c", E--H,NW); label("c", E--F); label("c", F--G,SE); label("c", G--H,SW); [/asy]](http://latex.artofproblemsolving.com/2/e/7/2e79de6673cd591bf38bff3efa048140bda61e9f.png)
![]() . ∎
. ∎
Pythagorean Triples
Pythagorean Triples are a group of integers a,b and c in which ![]() . These are the first few:
(3,4,5) (5,12,13) (7,24,25) (8,15,17)
. These are the first few:
(3,4,5) (5,12,13) (7,24,25) (8,15,17)
(9,40,41) (11,60,61) (12,35,37) (13,84,85)
(15,112,113) (16,63,65) (17,144,145) (19,180,181)
(20,21,29) (20,99,101) (21,220,221) (23,264,265)
(24,143,145) (25,312,313) (27,364,365) (28,45,53)
(28,195,197) (29,420,421) (31,480,481) (32,255,257)
(33,56,65) (33,544,545) (35,612,613) (36,77,85)
(36,323,325) (37,684,685)
And on and on...
Remember that if ![]() then
then ![]() so I did not include 6,8,10 or 10,24,26.
so I did not include 6,8,10 or 10,24,26.
Special Right triangles
45-90-45
Theorem
Say you have a right triangle with angles 45, 45 and 90. Then if ![]() (leg) is
(leg) is ![]() , then
, then ![]() (long side) is
(long side) is ![]()
Proof
If this triangle has two equal angles then it has two equal sides. Therefore we can make an equation: ![]() .
. ![]() means side and is the hypotenuse.
means side and is the hypotenuse. ![]() . We proved it!
. We proved it!
30-60-90
Theorem
If the angles of a right triangle are 30, 60 and 90, and if the short side is ![]() then the long side is
then the long side is ![]() and the other leg is
and the other leg is ![]() .
.
Proof
The long side is clearly ![]() because of the angles that are twice the size, so we can make an equation:
because of the angles that are twice the size, so we can make an equation: ![]() . t is the other leg.
. t is the other leg.
![]() We proved it!
We proved it!
Problem 1
Hawick is 15 miles south of Abbotsford, and Kelso is 17 miles east of Abbotsford. What is the distance from Hawick to Kelso?
Solution
![]()
Problem 2
A zip line starts on a platform that is 40 feet above the ground. The anchor for the zip line is 198 horizontal feet from the base of the platform. How long is the zip line?
Solution
![]()









