Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Talk:2021 USAMO Problems/Problem 1"

(Some ideas on this problem)
 
m (Latex formating fix)
 
(8 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
I spent some time poking around at this with the help of Geogebra, and after a few failed attempts (trying to figure out something from the relationship <math>\cot \alpha + \cot \beta + \cot \gamma = \cot \alpha \cot \beta \cot \gamma</math> when <math>\alpha + \beta + \gamma = \pi</math> and using applications of the Cosine rule to try to get something in terms of the triangle's angles) I realized that the point of concurrency is the intersection of the circumcircles of the three rectangles. The main difficulty after that is proving that this point is also the intersection point of the diagonals.
+
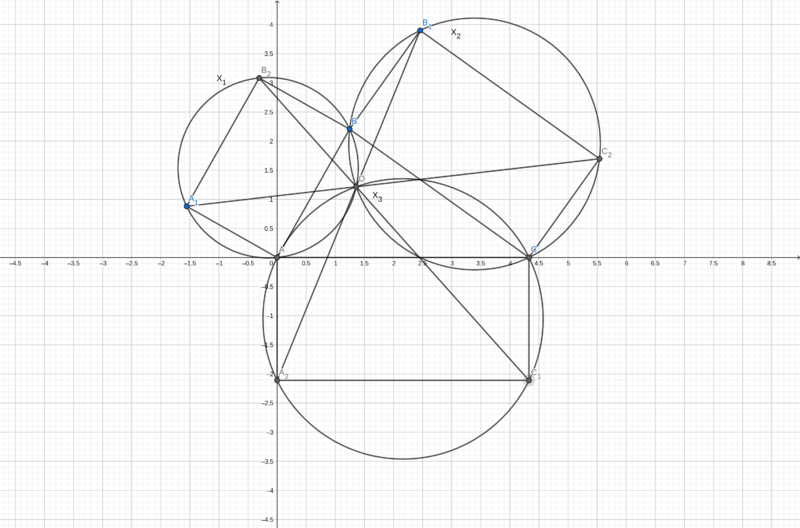
We are given the acute triangle <math>ABC</math>, rectangles <math>AA_1B_2B, BB_1C_2C, CC_1A_2A</math> such that <math>\angle AA_1B + \angle BB_1C + \angle CC_1A = \pi</math>. Let's call <math>\angle AA_1B = \alpha, \angle BB_1C = \beta, \angle CC_1A = \gamma</math>.
  
−
Clearly, if we construct two rectangles on <math>AB</math> and <math>BC</math> and then circumscribe them, the circles meet in two points, <math>B</math> and <math>O</math>. Equally clearly, the angles <math>|A_1OB_2| = |A_1AB_2| = |A_1BB_2| = \alpha</math> and <math>|B_1OC_2| = |B_1BC_2| = |B_1CC_2| = \beta</math>.
+
Construct circumcircles <math>X_1, X_2</math> around the rectangles <math>AA_1B_2B, BB_1C_2C</math> respectively. <math>X_1, X_2</math> intersect at two points: <math>B</math> and a second point we will label <math>O</math>. Now <math>A_1B</math> is a diameter of <math>X_1</math>, and <math>C_2B</math> is a diameter of <math>X_2</math>, so <math>\angle A_1OB = \angle C_2OB = \frac{\pi}{2}</math>, and <math>\angle A_1OC_2 = \pi</math>, so <math>O</math> is on the diagonal <math>A_1C_2</math>.
  
−
Now we can construct a circumcircle for the triangle <math>AOC</math> which will intersect the perpendiculars from <math>AC</math> at <math>A, C</math> in <math>A_2, C_1</math>, and <math>|A_2AC_1| = |A_2OC_1| = |A_2CC_1| = \gamma</math>. Now *if* the triples <math>(A_1,O,B_2), (C_1, O, B_2), (B_1, O, C_2)</math> are collinear, then the angle <math>|B_20C_1| = |A_2OC_1| = \gamma</math> and by construction <math>\alpha + \beta + \gamma = \pi</math> and we're done. But I can't figure out how to prove the collinearity (that is, to prove that the intersection of the circumcircles is on the diagonal).
+
<math>\angle A_1BB_2 = \angle A_1OB_2 = \alpha</math> (angles standing on the same arc of the circle <math>X1</math>), and similarly, <math>\angle B_1BC_2 = \angle B_1OC_2 = \beta</math>. Therefore, <math>\angle B_2OB_1 = \pi - (\alpha + \beta) = \gamma</math>.
 +
 
 +
Construct another circumcircle <math>X_3</math> around the triangle <math>AOC</math>, which intersects <math>AA_2</math> in <math>A'</math>, and <math>CC_1</math> in <math>C'</math>. We will prove that <math>A'=A_2, C'=C_1</math>. Note that <math>A'AOC</math> is a cyclic quadrilateral in <math>X_3</math>, so since <math>\angle A'AC = \frac{\pi}{2}</math>, <math>A'C</math> is a diameter of <math>X_3</math> and <math>\angle A'OC = \angle A'C'C = \frac{\pi}{2}</math> - so <math>A'ACC'</math> is a rectangle.
 +
 
 +
Since <math>\angle A'AC = \frac{\pi}{2}</math>, <math>A'C</math> is a diameter of <math>X_3</math>, and <math>\angle A'OC = \frac{\pi}{2}</math>. Similarly, <math>\angle B_1OC = \angle C'OA = \angle B_2OA = \frac{\pi}{2}</math>, so O is on <math>B_2C', B_1A'</math>, and by opposite angles, <math>\angle A'OC' = \gamma = \angle A'CC'</math>.
 +
 
 +
Finally, since <math>A'</math> is on <math>AA_2</math> and <math>C'</math> is on <math>CC_2</math>, that gives <math>\angle A_2AC' = \angle A_2CC_1</math> - meaning <math>C'</math> is on the line <math>AC_1</math>. But <math>C'</math> is also on the line <math>CC_1</math> - so <math>C'=C_1</math>. Similarly, <math>A'=A_2</math>. So the three diagonals <math>A_1C_2, B_1A_2, C_1B_2</math> intersect in <math>O</math>.
 +
 
 +
[[File:USAMO_Q1.png|alt="USAMO Q1 graph"|800px|USAMO 2021 Q1 set-up]]

Latest revision as of 14:14, 15 September 2021

We are given the acute triangle $ABC$, rectangles $AA_1B_2B, BB_1C_2C, CC_1A_2A$ such that $\angle AA_1B + \angle BB_1C + \angle CC_1A = \pi$. Let's call $\angle AA_1B = \alpha, \angle BB_1C = \beta, \angle CC_1A = \gamma$.

Construct circumcircles $X_1, X_2$ around the rectangles $AA_1B_2B, BB_1C_2C$ respectively. $X_1, X_2$ intersect at two points: $B$ and a second point we will label $O$. Now $A_1B$ is a diameter of $X_1$, and $C_2B$ is a diameter of $X_2$, so $\angle A_1OB = \angle C_2OB = \frac{\pi}{2}$, and $\angle A_1OC_2 = \pi$, so $O$ is on the diagonal $A_1C_2$.

$\angle A_1BB_2 = \angle A_1OB_2 = \alpha$ (angles standing on the same arc of the circle $X1$), and similarly, $\angle B_1BC_2 = \angle B_1OC_2 = \beta$. Therefore, $\angle B_2OB_1 = \pi - (\alpha + \beta) = \gamma$.

Construct another circumcircle $X_3$ around the triangle $AOC$, which intersects $AA_2$ in $A'$, and $CC_1$ in $C'$. We will prove that $A'=A_2, C'=C_1$. Note that $A'AOC$ is a cyclic quadrilateral in $X_3$, so since $\angle A'AC = \frac{\pi}{2}$, $A'C$ is a diameter of $X_3$ and $\angle A'OC = \angle A'C'C = \frac{\pi}{2}$ - so $A'ACC'$ is a rectangle.

Since $\angle A'AC = \frac{\pi}{2}$, $A'C$ is a diameter of $X_3$, and $\angle A'OC = \frac{\pi}{2}$. Similarly, $\angle B_1OC = \angle C'OA = \angle B_2OA = \frac{\pi}{2}$, so O is on $B_2C', B_1A'$, and by opposite angles, $\angle A'OC' = \gamma = \angle A'CC'$.

Finally, since $A'$ is on $AA_2$ and $C'$ is on $CC_2$, that gives $\angle A_2AC' = \angle A_2CC_1$ - meaning $C'$ is on the line $AC_1$. But $C'$ is also on the line $CC_1$ - so $C'=C_1$. Similarly, $A'=A_2$. So the three diagonals $A_1C_2, B_1A_2, C_1B_2$ intersect in $O$.

"USAMO Q1 graph"

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Talk:2021_USAMO_Problems/Problem_1&oldid=162296"