Trigonometric identities
Trigonometric identities are used to manipulate trig equations in certain ways. Here is a list of them:
Contents
Basic Definitions
The six basic trigonometric functions can be defined using a right triangle:
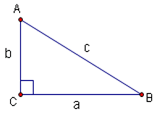
The six trig functions are sine, cosine, tangent, cosecant, secant, and cotangent. They are abbreviated by using the first three letters of their name (except for cosecant which uses ![]() ). They are defined as follows:
). They are defined as follows:
Reciprocal Relations
From the last section, it is easy to see that the following hold:
Pythagorean Identities
Angle Addition Identities
Even-Odd Identities
Prosthaphaersis Indentities
(Otherwise known as sum-to-product identities)
Other Identities
See also
This article is a stub. Help us out by expanding it.









