Need help finding a book? Have questions about particular items?
Click here to Ask AoPS!Calculus links & errata
Below are some of the links that are referenced in the book Calculus. (Note: Art of Problem Solving is not responsible for the content on any external site.)
If you have suggestions for other links, please email books@artofproblemsolving.com.
Links to Contests
William Lowell Putnam Competition
Harvard-MIT Mathematics Tournament
MIT Integration Bee (2017 site)
Links to AoPS pages
Links to Other Websites
Unfortunately, the book is not perfect. If you find an error in the text or solutions that's not already listed below, we would appreciate a short e-mail to books@artofproblemsolving.com describing the error.
Errors in the Textbook:
- Chapter 4, Problem 4.51: The final two sentences of this problem should read "Show that for any z > a, we have |E(z)| ≤ M(z-a)^2, where M is the maximum value of |f"(x)| on the interval [a,z]. (In fact, later in the book, we will show that |E(z)| ≤ ½M(z-a)^2, but this is difficult with our current technology.)"
Errors in the Solutions Manual:
- Chapter 8, Problem 8.2.1c: The numerator 4 sin π/2 cos π/4 and the denominator 4 sin π/2 sin π/4 should be flipped so the numerator is 4 sin π/2 sin π/4 and the denominator is 4 sin π/2 cos π/4. The next line should be tan π/4.
The following errors were corrected in the 2017 printing.
Textbook
- Section 2.1, Problem 2.4, top of p.41: f(x) is missing from the limit in the first paragraph.
- Section 3.3, Problem 3.11: the references to the previous problems are incorrect. The first reference is to Problem 3.9 and the second reference is to the note after Problem 3.9.
- Section 3.4, box at top of p.76: last line should be f'(f^-1(x)).
- Section 4.2, Problem 4.17, p.104, 2nd paragraph of solution: "...angle theta with the corner,..."
- Section 4.4, paragraph after Problem 4.23, p. 111: "One nice advantage..."
- Section 4.5, Problem 4.28, p.115: Delta is 23-32 = -9.
- Section 5.3, Concept box on p.159: "...whenever we see a term..."
- Section 5.3.7, Problem 5.35, p. 164: at the end of the third paragraph, there should be a "d theta" at the end of the expression for dx.
- Section 5.A, p. 187: Before the definition, positive is missspelled.
- Section 6.4, Problem 6.14, p.205: the three displayed equations that have limits y -> infinity should instead be x -> infinity. Also the limit is 1/(1+1/x).
- Section 7.3, Problem 7.16, p.235: the series is undefined at the n=1 term, so the series should start at n=2.
- References, p.303: "...after this book"
Solutions Manual
- Problem 1.5.2(a): Final answer is missing a left parenthesis.
- Problem 1.39: There are a couple of minus signs missing in the displayed equations, before pi/8 and pi/5.
- Problem 3.6.5: The solution has a flaw, because we can't divide by cos theta at points where it's 0. So we've only proved that the derivative of cos is -sin wherever cos is nonzero. If we assume that the derivative is continuous, then we can fill in the missing points. (Thanks to Luke Robitaille for pointing this out.)
- Problem 4.6.3: The formula for V should have (x/2)3.
- Problem 5.3.1(t): dx = 3u^2 du.
- Problem 5.54(k): The final answer is coth^(-1), the inverse of the hyperbolic cotangent function.
- Problem 6.1.1(c), 2nd sentence: first < should be <=.
- Problem 7.2.1(b), 2nd displayed equation: the A and B should not be inside the parentheses in the second expression.
- Problem 7.4.1(b): the series converges to -pi^2/12.
- Problem 7.4.2: The conditions on a_n are only for n > N.
- Problem 7.6.4: The first equation in the "simpler solution" has x^4 in the numerator of the final term.
- Problem 9.2.4: The final solution should have e^(-x) instead of e^x.
The following errors were corrected in the 2015 printing.
Textbook
- Section 2.1, Problem 2.9(a), page 46: the limit in the second line of the solution should be x -> 0, not x -> a.
- Section 2.A, page 55, second paragraph: the limit should be z, not y.
- Section 3.5, page 79, right before Problem 3.23: we get a very useful theorem.
- Problem 5.64, page 184: you should assume that f(x) is nonnegative.
- Section 5.A, Problem 5.76, page 186: the references to the parts are incorrect: part (c) should refer to part (b) instead of (a), and part (d) should refers to parts (b) and (c), not (a) and (b).
- Section 6.2, definition at top of page 197: the "R" is in the wrong font.
- Section 7.4, Exercise 7.4.2, page 241: the word "absolutely" is missing from the problem statement -- the result is true only if the original series is absolutely convergent.
- Problem 9.1.6: The equation for the homogeneous differential equation should be in the form y' = f(y/x). Following that, the right side can be written as 1/2 ( 1/(y/x) + y/x ).
Solutions Manual
- Problem 1.5.1: The problem also asked to find the ranges, but this are missing from the solution. The ranges of sec and csc are (-∞,-1] ∪ [1,∞), and the range of cot is all of R.
- Problem 2.1.3: The given proof only works for c positive. Replacing c with |c| whenever it appears on the right side of an inequality makes the proof work for negative c as well. If c=0 the proof doesn't work, but the result is obvious in that case (the limit of the 0 function is always 0).
- Problem 3.6.4: The problem asked for the slope of the tangent line, so the final answer should be 1 - 2/π.
- Problem 4.2.7: The inequalities near the end of the solution are reversed: the derivative is positive for x < 15*sqrt(11) and negative for x > 15*sqrt(11).
- Problem 5.64: The arc length approximation is missing an (xi+i-xi) term, so that the sum becomes a Riemann sum.
- Problem 8.21(d): The motion is clockwise, so there should be a minus sign in the y-coordinate of the final answer.
- Problem 8.29: The second and third integrals displayed should end in dτ, not dt.
- Problem 9.28(c), 2nd paragraph: The inequality for c should read 0 < c < 1.
The errors below were all in the first edition, but have been corrected in the second edition (published in 2013).
Textbook
- Section 1.5, page 24: in the definition of "Periodic", should read: "...if there exists a positive real number...".
- Section 1.7, page 30: in parenthetical note to solution to part (d): "...is nontrivial to prove at this stage,..".
- Section 2.1, page 38: parenthetical note near top: "...are used throughout calculus in this context,...".
- Section 2.1, page 38: a bit past halfway down the page, refers to "diagram on the right on the next page"; the diagram is actually on the same page.
- Section 2.1, page 40: sentence beginning with "However,..." should be |3z2 + 12z| ≤ |3z2| + |12z| = ..., and on the next line, 3δ2 + 12δ = 3δ(4+δ).
- Section 2.1, page 41: the paragraph beginning "Yet another way..." is completely incorrect. It should read:
Yet another way to see this is to appeal to the δ-ε definition. For any ε > 0, we can choose 0 < δ < ε, since
0 < |x-0| < δ => |f(x) - 0| = |x - 0| < δ < ε. - Section 3.5, page 79, paragraph after "Important" box: "...if a continuous function on [a,b] starts and ends..."
- Section 3.7, page 82: in the Quotient Rule, the left side should be (f/g)'(x).
- Problem 3.34, page 84: a should be a positive real number.
- Section 4.3, page 106: near the bottom, should be "This is the time at which the particle switches from...".
- Section 4.4, Problem 4.22, page 111: "Let f be a differentiable function..."
- Section 4.5, page 115: at the very bottom, in the f''(x) expression, the exponent of x should be -9/5.
- Section 4.6, page 121: Unfortunately the solution has multiple errors. You should replace page 121 with this page, and ignore the sentence at the top of page 122.
- Section 5.1, page 133, last line: inequalities are reversed, should be
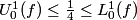
- Section 6.5, page 207, first paragraph of solution to Problem 6.16: "...region to the left of x = b..."
- Section 7.3, page 234, example after the Integral Test and the Warning: the function 1/2^x is (1/2)^x, not (1/2)^(-x) as printed. So the entire computation should be (with an extra step added for a little more clarity):
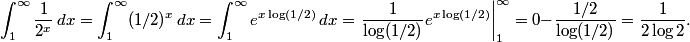
(Thanks to reader Nathan Phan for noticing this error.) - Section 8.2, page 270: we should be substituting y/r for sin(theta), not x/r
- Section 9.1, page 284: in the "Warning" box, the first sentence should read: "Even though we are treating dx and dy as variable terms,...".
Solutions Manual
- Problem 2.16(c): The quantity should be lim_(x -> 1) 1/(1+sqrt(x)), and the answer should be 1/2.
- Problem 3.6.1: The implicit differentiation should be 2x - 2yy' = 0, so y' = x/y. The final answer is 2/sqrt(3).
- Problem 3.29: The last term of the final answer should be sqrt(3).
- Problem 4.2.5: The substitution at the start of the second paragraph should be
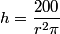 .
This changes the final answer to having a cube-root of π where it currently has just π, and the final answer is
.
This changes the final answer to having a cube-root of π where it currently has just π, and the final answer is 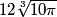 , or about 37.86 cents.
, or about 37.86 cents. - Problem 4.6.1: In the next-to-last sentence we are actually considering the moment when sin(θ)=10/15 so csc2(θ)=2.25. This changes the final answer to 2/225.
- Problem 4.6.2: The answer should read -(100)(.1)/2=-5 instead of -50. The volume decreases at a rate of 5 cm3/min.
- Problem 7.1.1(c): It should be n/(n2+1) ≤ n/n2 = 1/n, and then on the next line it is 1/n that goes to 0.





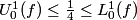
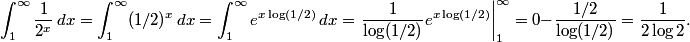
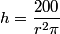 .
This changes the final answer to having a cube-root of π where it currently has just π, and the final answer is
.
This changes the final answer to having a cube-root of π where it currently has just π, and the final answer is 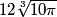 , or about 37.86 cents.
, or about 37.86 cents.



