1965 IMO Problems/Problem 6
Contents
Problem
In a plane a set of ![]() points (
points (![]() ) is given. Each pair of points is connected by a segment. Let
) is given. Each pair of points is connected by a segment. Let ![]() be the length of the longest of these segments. We define a diameter of the set to be any connecting segment of length
be the length of the longest of these segments. We define a diameter of the set to be any connecting segment of length ![]() . Prove that the number of diameters of the given set is at most
. Prove that the number of diameters of the given set is at most ![]() .
.
Solution
Image of problem Solution. Credits to user awe-sum.
Remarks (added by pf02, October 2024)
1. As a public service, I will upload the "Image of problem Solution" mentioned above to this web page. That way, a reader can see the "Solution" immediately, without having to go to another web site, and we are not subjected to the possibility of the imgur.com website being taken down, or Imgur's parent company deciding to delete this particular image. Credits for the image are due to user awe-sum, as pointed out above.
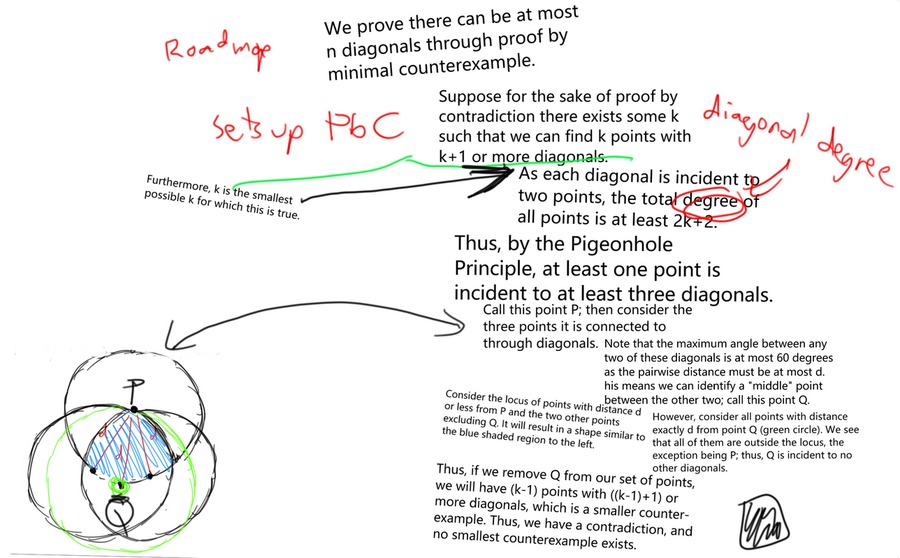
2. This "Solution" is presented very badly, and edited very badly. Indeed, some terms are undefined, left to the reader to make sense of (e.g. "incident", "degree"). But let us be forgiving, and let us do our best to make sense of the "Solution".
3. The "Solution" is incomplete, to the point of not being a solution at all. There are some serious gaps, which raise questions which are not addressed, and a reader can not be expected to fill in the details. These are:
a. The author says "... at least one point is incident to at least three diagonals". But, it could also happen that two points are "incident" to two "diagonals" (i.e. diameters) each. The author does not address this possibility at all.
b. The author says "consider all points at distance exactly d from point Q (the green circle). We see that all of them are outside the locus, the exception being P." This is far from obvious. It assumes that all the other k-4 points (those points of the k given points which are not highlighted in the picture) are inside the "locus (the blue shaded region)". In fact, it seems to this reader that this is not necessarily true.
c. Another issue with this "Solution" is that it assumes ![]() , while the
statement of the problem has
, while the
statement of the problem has ![]() . This shortcoming is easy to fix,
unlike the previous two I mentioned.
. This shortcoming is easy to fix,
unlike the previous two I mentioned.
4. I will give two solutions below, in the section "Solution 2" and "Section 3".
Solution (by user awe-sum)
Solution 2
![]() For the purpose of this proof, let us define an
For the purpose of this proof, let us define an
![]() as the shape we obtain when we take a triangle
as the shape we obtain when we take a triangle
![]() in which we replace the side
in which we replace the side ![]() by the
by the ![]() arc of the
circle centered at
arc of the
circle centered at ![]() with radius
with radius ![]() , going from
, going from ![]() to
to ![]() , and
similarly for the other two sides
, and
similarly for the other two sides ![]() and
and ![]() .
.
See the picture below.
Note that if the sides of the original equilateral triangle were of length
![]() , then the distance from a vertex to any point on the opposite arc is
, then the distance from a vertex to any point on the opposite arc is ![]() .
Also, the distance between any two points on the arcs, such that none of them
are vertices is
.
Also, the distance between any two points on the arcs, such that none of them
are vertices is ![]() . And finally, the distance from a vertex to any point
on the arcs adjacent to it (which is not another vertex) is
. And finally, the distance from a vertex to any point
on the arcs adjacent to it (which is not another vertex) is ![]() .
.
![]() A configuration of
A configuration of ![]() points has exactly
points has exactly ![]() diameters
if an only if
diameters
if an only if ![]() of the points are the vertices of an equilateral arc
triangle, and the other
of the points are the vertices of an equilateral arc
triangle, and the other ![]() are on the boundary of the triangle.
are on the boundary of the triangle.
In the configuration shown above, we have ![]() points with
points with ![]() diameters.
diameters.
![]() It is clear that if we have a configuration
as described in the lemma then there are
It is clear that if we have a configuration
as described in the lemma then there are ![]() diameters. We will prove the
converse by induction. We want to prove that if we have a configuration
of
diameters. We will prove the
converse by induction. We want to prove that if we have a configuration
of ![]() points with
points with ![]() diameters, then the points are in a configuration
as described above.
diameters, then the points are in a configuration
as described above.
If ![]() it is clear that the
it is clear that the ![]() points have to be the vertices of an
equilateral triangle since the sides are equal (to
points have to be the vertices of an
equilateral triangle since the sides are equal (to ![]() ). Assume we know
the statement to be true for
). Assume we know
the statement to be true for ![]() , and prove it for
, and prove it for ![]() . Assume that
we have
. Assume that
we have ![]() points with
points with ![]() diameters
diameters ![]() . Consider
. Consider ![]() of the
points, and let
of the
points, and let ![]() be the remaining point. It follows from the induction
hypothesis that
be the remaining point. It follows from the induction
hypothesis that ![]() of the
of the ![]() are the vertices of an equilateral arc
triangle, and the other
are the vertices of an equilateral arc
triangle, and the other ![]() are on the boundary.
are on the boundary.
Now let us examine where ![]() may be. It can not be outside of the equilateral
arc triangle because then the distance to at least one of the vertices would
be
may be. It can not be outside of the equilateral
arc triangle because then the distance to at least one of the vertices would
be ![]() , and the diameter of the set would be
, and the diameter of the set would be ![]() rather than
rather than ![]() . It
can not be inside the triangle because then all the distances from
. It
can not be inside the triangle because then all the distances from ![]() to the
to the
![]() points considered are
points considered are ![]() , and we would not have
, and we would not have ![]() diameters, as
assumed. So
diameters, as
assumed. So ![]() must be on the boundary of the equilateral arc triangle,
which proves the induction step, and the lemma.
must be on the boundary of the equilateral arc triangle,
which proves the induction step, and the lemma.
Now the solution to the problem is easy to finish. Assume we have ![]() points
given, and the configuration has
points
given, and the configuration has ![]() diameters. I claim that we can not have
diameters. I claim that we can not have
![]() . We prove this by contradiction. If we did, let us consider a set
. We prove this by contradiction. If we did, let us consider a set
![]() consisting of only
consisting of only ![]() of the diameters. Because of the lemma, this
implies that the
of the diameters. Because of the lemma, this
implies that the ![]() points form a configuration as described in the lemma,
i.e.
points form a configuration as described in the lemma,
i.e. ![]() of them are the vertices of an equilateral arc triangle, and the
other
of them are the vertices of an equilateral arc triangle, and the
other ![]() are on the boundary. Now consider a diameter
are on the boundary. Now consider a diameter ![]() which is
not in
which is
not in ![]() . It is the distance of a segment between two of the points
. It is the distance of a segment between two of the points
![]() in the configuration. If one of
in the configuration. If one of ![]() is a vertex, then
this diameter
is a vertex, then
this diameter ![]() is in
is in ![]() , which is a contradiction. If none of
, which is a contradiction. If none of
![]() are vertices, then the length of
are vertices, then the length of ![]() , so
, so ![]() is not a diameter, which is again a contradiction.
is not a diameter, which is again a contradiction.
It follows that ![]() which proves the problem.
which proves the problem.
[Solution by pf02, October 2024]
Solution 3
See Proposition 2.3 on page 19 in "Lecture Notes: Combinatorics in the Plane" by Torsten Ueckerdt, from March 12, 2015 at https://www.math.kit.edu/iag6/lehre/combplane2013s/media/lecture_notes.pdf .
See Also
| 1965 IMO (Problems) • Resources | ||
| Preceded by Problem 5 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Last Question |
| All IMO Problems and Solutions | ||