2001 AIME I Problems/Problem 13
Problem
In a certain circle, the chord of a ![]() -degree arc is
-degree arc is ![]() centimeters long, and the chord of a
centimeters long, and the chord of a ![]() -degree arc is
-degree arc is ![]() centimeters longer than the chord of a
centimeters longer than the chord of a ![]() -degree arc, where
-degree arc, where ![]() The length of the chord of a
The length of the chord of a ![]() -degree arc is
-degree arc is ![]() centimeters, where
centimeters, where ![]() and
and ![]() are positive integers. Find
are positive integers. Find ![]()
Solution
Solution 1
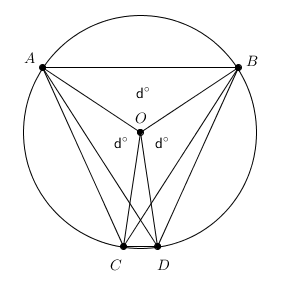
Note that a cyclic quadrilateral in the form of an isosceles trapezoid can be formed from three chords of three ![]() -degree arcs and one chord of one
-degree arcs and one chord of one ![]() -degree arc. The diagonals of this trapezoid turn out to be two chords of two
-degree arc. The diagonals of this trapezoid turn out to be two chords of two ![]() -degree arcs. Let
-degree arcs. Let ![]() ,
, ![]() , and
, and ![]() be the chords of the
be the chords of the ![]() -degree arcs, and let
-degree arcs, and let ![]() be the chord of the
be the chord of the ![]() -degree arc. Also let
-degree arc. Also let ![]() be equal to the chord length of the
be equal to the chord length of the ![]() -degree arc. Hence, the length of the chords,
-degree arc. Hence, the length of the chords, ![]() and
and ![]() , of the
, of the ![]() -degree arcs can be represented as
-degree arcs can be represented as ![]() , as given in the problem.
, as given in the problem.
Using Ptolemy's theorem,
![]()
![]()
![]()
![]()
We can then apply the quadratic formula to find the positive root to this equation since polygons obviously cannot have sides of negative length.
![]()
![]()
![]() simplifies to
simplifies to ![]() which equals
which equals ![]() Thus, the answer is
Thus, the answer is ![]() .
.
Solution 2
Let ![]() and
and ![]() be the circumradius. From the given information,
be the circumradius. From the given information, ![]()
![]() Dividing the latter by the former,
Dividing the latter by the former, ![]()
![]() We want to find
We want to find ![]() From
From ![]() this is equivalent to
this is equivalent to ![]() Using the quadratic formula, we find that the desired length is equal to
Using the quadratic formula, we find that the desired length is equal to ![]() so our answer is
so our answer is ![]()
Solution 3
Let ![]() ,
, ![]() be the circumradius, and
be the circumradius, and ![]() be the length of 3d degree chord. Using the extended sine law, we obtain:
be the length of 3d degree chord. Using the extended sine law, we obtain:
![]()
![]()
![]() Dividing the second from the first we get
Dividing the second from the first we get ![]() By the triple angle formula we can manipulate the third equation as follows:
By the triple angle formula we can manipulate the third equation as follows: ![]() Solving the quadratic equation gives the answer to be
Solving the quadratic equation gives the answer to be ![]() .
.
See also
| 2001 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()









