2003 AMC 8 Problems/Problem 23
Contents
[hide]Problem
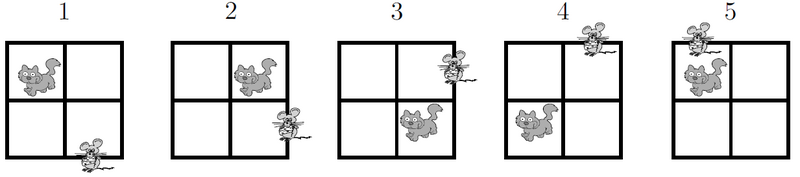
In the pattern below, the cat moves clockwise through the four squares, and the mouse moves counterclockwise through the eight exterior segments of the four squares.
If the pattern is continued, where would the cat and mouse be after the 247th move?
Solution
Break this problem into two parts: where the cat will be after the ![]() move, and where the mouse will be.
move, and where the mouse will be.
The cat has four possible positions in 1 cycle which are repeated every four moves. ![]() has a remainder of
has a remainder of ![]() when divided by
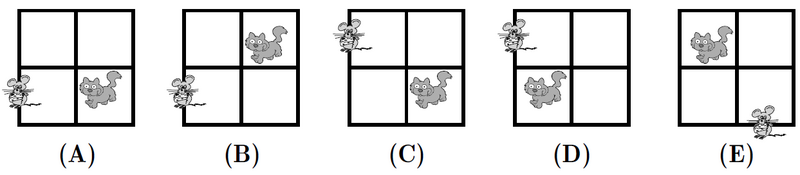
when divided by ![]() . This corresponds to the position the cat has after the 3rd move, which is the bottom right corner.
. This corresponds to the position the cat has after the 3rd move, which is the bottom right corner.
Similarly, the mouse has eight possible positions in 1 cycle that repeat every eight moves. ![]() has a remainder of
has a remainder of ![]() when divided by
when divided by ![]() . This corresponds to the position the mouse has after the 7th move which is bottom left corner.
. This corresponds to the position the mouse has after the 7th move which is bottom left corner.
The only arrangement with the mouse in that position and the cat in the bottom right square is ![]() .
.
Video Solution
https://www.youtube.com/watch?v=OxtaQkcJDfU ~David
See Also
| 2003 AMC 8 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AJHSME/AMC 8 Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()