2004 AMC 12A Problems/Problem 12
Problem
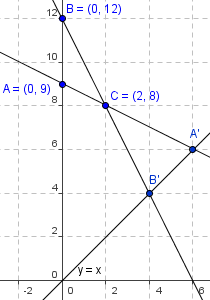
Let ![]() and
and ![]() . Points
. Points ![]() and
and ![]() are on the line
are on the line ![]() , and
, and ![]() and
and ![]() intersect at
intersect at ![]() . What is the length of
. What is the length of ![]() ?
?
![]()
Solution
The equation of ![]() can be found using points
can be found using points ![]() to be
to be ![]() . Similarily,
. Similarily, ![]() has the equation
has the equation ![]() . These two equations intersect the line
. These two equations intersect the line ![]() at
at ![]() and
and ![]() . Using the distance formula or
. Using the distance formula or ![]() right triangles, the answer is
right triangles, the answer is ![]() .
.
See also
| 2004 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 11 |
Followed by Problem 13 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()