2007 IMO Shortlist Problems/G3
IMO 2007 Short list/G3
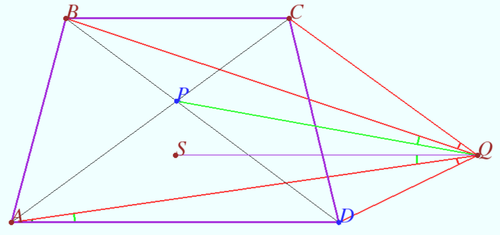
The diagonals of a trapezoid 
intersect at point 
Point 
lies between the parallel lines 
and 
such that 
and line 
separates points 
and 
Prove that 
Proof
and 
are isogonals with respect 
is isogonal to 
with respect
From the converse of The isogonal theorem we get
vladimir.shelomovskii@gmail.com, vvsss
